Матричное представление трёхмерных преобразований.

Точка представляется тремя координатами P(x,y,z). В однородных координатах:

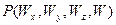
Соответственно матрица преобразования будет иметь вид:

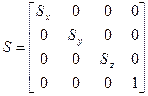
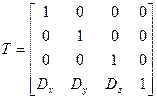
Поворот выполняют на основе некоторых принятых соглашений:

1) Ось вращения – OX. Положительное направление от оси OY к OZ.

2) Ось вращения – OY. Положительное направление от оси OZ к OX.

3) Ось вращения – OZ. Положительное направление от оси OX к OY.

И всегда оговаривается, что OZ перпендикулярна плоскости экрана/бумаги. Поворот в трёхмерном пространстве состоит как бы из трёх ступеней:

1) Поворот вокруг оси OZ (угол поворота обозначается a)

2) Поворот вокруг оси OX (угол поворота обозначается b)

3) Поворот вокруг оси OY (угол поворота обозначается g)

Поворот в трёхмерном пространстве описывается матрицей поворота R, где

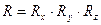, где матрица отдельных поворотов имеет вид:

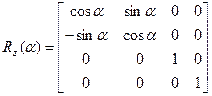
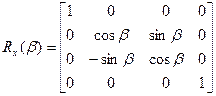
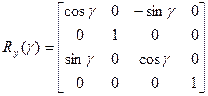
Когда не успевают по быстродействию, то можно выполнить с помощью следующей матрицы:

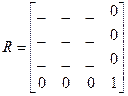, где _ – частные произведения.

Имеет смысл использовать в тех случаях, когда это необходимо для обеспечения в режиме отображения. Это всё справедливо относительно начала координат. Относительно произвольной точки, формула будет иметь вид:

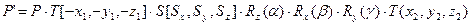
Реально при использовании таких формул мы получаем абсолютно корректные преобразования. Ошибки чаще всего связаны с неправильным определением знаков и величин углов a, b, g.