Основы теории проверки статистических гипотез. Непараметрические критерии.
1. Статистические критерии делятся на параметрические и непараметрические.
Параметрические критерии предполагают наличие нормального распределения в сравниваемых выборках и используют в процессе расчета параметры распределения (средние, дисперсии, среднее квадратическое отклонение). Например: t-критерий Стьюдента, F-критерий Фишера и др.
Непараметрические критерии не предполагают нормального распределения в сравниваемых выборках и используют в процессе расчета ранги значений признака. Например, критерий Манна-Уитни, критерий Уилкоксона, критерий знаков и др.).
Ранг - порядковый номер значения признака.
2. Для каждого параметрического критерия имеется, по крайней мере, один непараметрический аналог.
Аналогом двухвыборочного t-критерия Стьюдента является U-критерий Манна-Уитни. Аналогом парного t-критерия Стьюдента является W-критерий Уилкоксона.
U-критерий Манна-Уитни - непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно.
Данный метод выявления различий между выборками был предложен в 1945 г. американским химиком и статистиком Ф. Уилкоксоном (рисунок 3.1, а). В 1947 г. метод был переработан и расширен математиками Х.Б. Манном и Д.Р. Уитни (рисунок 3.1, b).


a b
Рисунок 3.1. а - Ф. Уилкоксон, b - Х.Б. Манн
U-критерий подходит для сравнения малых выборок. В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти (n1, n2≥3 или n1=2, n2≥5).
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа разные) или очень малое число таких совпадений.
W-критерий Уилкоксона - непараметрический статистический критерий, используемый для сравнения двух зависимых выборок по уровню какого-либо признака, измеренного количественно.
Критерий Уилкоксона применяется в случае, если объем выборки «n» удовлетворяет неравенству 5≤n≤50.
3. Схема применения критерия Манна-Уитни:
1) Н0: 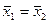 .
.
Н1: 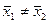 .
.
2) р=0,05 - уровень значимости.
3) Из двух сравниваемых выборок составляется единый ранжированный ряд.
Единый ранжированный ряд разделяется на два, состоящих из единиц первой и второй выборок, при этом отмечаются значения рангов для каждой единицы.
Подсчитывается отдельно сумма рангов, выпавших на долю элементов первой выборки, и отдельно - на долю элементов второй выборки.
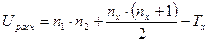 , (3.1)
, (3.1)
где Tx - большая из двух ранговых сумм, nx - объем выборки, соответствующий Tx, n1, n2 - объемы рассматриваемых выборок.
4) Uтабл ( 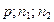 ).
).
5) Если 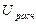 >
> 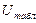 , то «H0» принимается.
, то «H0» принимается.
Если 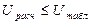 , то «H0» отвергается.
, то «H0» отвергается.
Пример 3.1. Исследуется эффективность препарата, позволяющего сбросить лишнюю массу больным, страдающим ожирением. При этом группе добровольцев предписана определенная диета.
Через месяц, с целью проверки соблюдения диеты и регулярного приема препарата, фиксируется величина потерянной массы (кг). Для проведения эксперимента отобрана группа из 8 человек. 3 из них получали исследуемый препарат (экспериментальная группа), а 5 получали плацебо (контрольная группа). Отбор 3 испытуемых из 8 в экспериментальную группу осуществлялся случайным образом. Все участники эксперимента считали, что принимают препарат.
| Экспериментальная группа | Контрольная группа |
| Потерянная масса, кг | Потерянная масса, кг |
| 6,2 | 4,0 |
| 3,0 | -0,5 |
| 3,9 | 3,3 |
| 1,5 | |
| 3,0 |
Решение.
1) Н0: 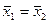 .
.
Н1: 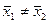 .
.
a. р=0,05 - уровень значимости.
b. Составим единый ряд.
| Потерянная масса, кг | 6,2 | 3,0 | 3,9 | 4,0 | -0,5 | 3,3 | 1,5 | 3,0 |
| Ранг | 3,5 | 3,5 |
Разделим единый ранжированный ряд на два, состоящих из единиц первой и второй выборок.
| Экспериментальная группа | Контрольная группа | ||
| Потерянная масса, кг | Ранг | Потерянная масса, кг | Ранг |
| 6,2 | 4,0 | ||
| 3,0 | 3,5 | -0,5 | |
| 3,9 | 3,3 | ||
| 1,5 | |||
| 3,0 | 3,5 | ||
| Т1=17,5 | Т2=18,5 |
Т1 и Т2 – суммы рангов; Т1< Т2, значит Т2= Тх , nx=n2=5.
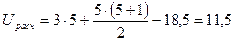 .
.
c. Uтабл ( 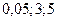 )=1.
)=1.
d. 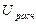 >
> 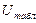 , то «H0» принимается, т.е. препарат неэффективен.
, то «H0» принимается, т.е. препарат неэффективен.
4. Схема применения критерия Уилкоксона:
1) Н0: 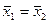 .
.
Н1: 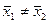 .
.
2) р≈0,05 - уровень значимости.
3) Вычисляется разность между индивидуальными значениями во втором и первом замерах.
Абсолютные величины разностей упорядочиваются по рангу (меньшему значению присваивается меньший ранг).
Каждому рангу ставится знак «+» или «–» в зависимости от знака соответствующей ему разности, получаются знаковые ранги.
Расчетное значение критерия Wрасч определяется из суммы знаковых рангов.
4)Wтабл ( 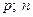 ), где n - объем выборки.
), где n - объем выборки.
5) Если 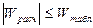 , то «H0» принимается.
, то «H0» принимается.
Если 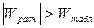 , то «H0» отвергается.
, то «H0» отвергается.
Пример 3.2. Проверить есть ли разница в содержании сахара в крови натощак до работы и через три часа после работы у 12 работающих на ультразвуковых установках.
| № | Содержание сахара до работы | Содержание сахара после работы |
Решение.
1) Н0: 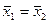 .
.
Н1: 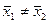 .
.
2) р≈0,05 - уровень значимости.
3)
| № | Х | у | х-у | 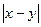
| 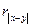
| Знаковые ранги |
| 4,5 | 4,5 | |||||
| -2 | -2 | |||||
| 4,5 | 4,5 | |||||
| Сумма знаковых рангов | Wрасч =74 |
4) Wтабл ( 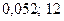 )=50.
)=50.
5) 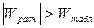 , то «H0» отвергается, значит есть разница в содержании сахара в крови у работников до и после работы.
, то «H0» отвергается, значит есть разница в содержании сахара в крови у работников до и после работы.
5. В биостатистике часто проверяются гипотезы о виде распределения случайной величины.
Множество биологических и медицинских показателей (показатели физического развития, составляющие плазмы крови и др.), а также ошибки их измерения подчиняются нормальному распределению.
Поэтому важно уметь проверять гипотезы о параметрах нормально распределенных случайных величин.
Все предположения о характере того или иного распределения - являются гипотезами. Поэтому они должны подвергаться статистической проверке с помощью критериев согласия. Эти критерии дают возможность определить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными, т.е. случайными, а когда – существенными, т.е. неслучайными.
Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду.
Наиболее распространенными критериями согласия являются критерии χ2-Пирсона и Колмогорова-Смирнова.
Эти критерии применяются в двух случаях:
· для сопоставления расчетного распределения признака с теоретическим распределением (нормальным, показательным, равномерным и т.д.) (рисунок 3.2);
· для сопоставления двух расчетных распределений одного и того же признака.
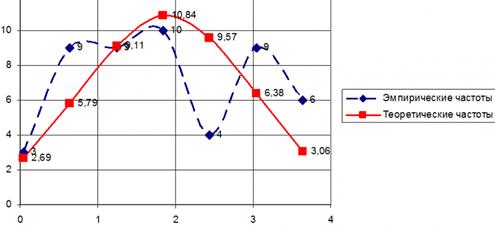
Рисунок 3.2. Сопоставление эмпирических и теоретических частот
6. Схема применения критерия согласия χ2- Пирсона:
1) Н0: случайная величина «Х» имеет функцию распределения F(x).
H1: случайная величина «Х» не имеет функцию распределения F(x).
2) р=0,05- уровень значимости.
3) 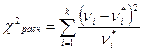 , (3.2)
, (3.2)
где k - число групп, на которое разбито эмпирическое распределение, 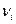 - наблюдаемая частота признака в i-й группе,
- наблюдаемая частота признака в i-й группе, 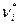 - теоретическая частота.
- теоретическая частота.
4) χ2табл ( 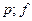 ),
),
где 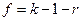 - число степеней свободы (табличное значение), k - число групп выборки, r - число параметров предполагаемого распределения (для нормального распределения r=2).
- число степеней свободы (табличное значение), k - число групп выборки, r - число параметров предполагаемого распределения (для нормального распределения r=2).
5) Если 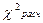 ≤
≤ 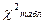 , то «H0» принимается.
, то «H0» принимается.
Если 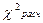 >
> 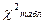 , то «H0» отвергается.
, то «H0» отвергается.
Критерий согласия Пирсона применяется при большом числе наблюдений (n>30), при этом частота каждой группы должна быть не менее пяти.
7. Схема применения критерия согласия Колмогорова - Смирнова:
1) Н0: случайная величина «Х» имеет функцию распределения F(x).
H1: случайная величина «Х» не имеет функцию распределения F(x).
2) р=0,05- уровень значимости.
3) 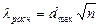 , (3.3)
, (3.3)
где 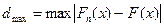 - максимальное значение абсолютной величины разности между наблюдаемой функцией распределения Fn(x) и соответствующей теоретической функцией распределения F(x), n - число наблюдений в статистическом ряду.
- максимальное значение абсолютной величины разности между наблюдаемой функцией распределения Fn(x) и соответствующей теоретической функцией распределения F(x), n - число наблюдений в статистическом ряду.
4) λтабл=1,36 (табличное значение).
5) Если 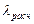 ≤
≤ 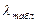 , то «H0» принимается.
, то «H0» принимается.
Если 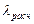 >
> 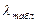 , то «H0» отвергается.
, то «H0» отвергается.
Критерий Колмогорова-Смирнова применяется при большом числе наблюдений (n>30).
5. Литература:
1. Герасимов А.Н. Медицинская статистика: Учеб. Пособие. – М.: МИА, 2007. - 480 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов.- 9-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
3. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах/ Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
4. http://matstats.ru/
Дата добавления: 2016-10-07; просмотров: 3448;











