Вынужденные колебания. Резонанс. Резонансные кривые.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью вынуждающей силы, изменяющейся по гармоническому закону:

F = F_m cos wt,

где w - циклическая частота вынуждающей силы.

Дифференциальное уравнение для вынужденных колебаний имеет вид

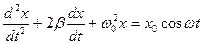. (1)

Здесь x – смещение колеблющейся точки относительно положения равновесия, b- коэффициент затухания, w₀ - циклическая частота собственных колебаний.

В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими. Решение уравнения (1) для установившегося режима имеет вид

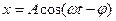. (2)

Причем амплитуда A и фаза j зависят от w, w₀, b, x₀

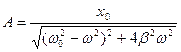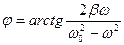, . (3)

Амплитудные резонансные кривые построенные на основе (3), приведены на рис.1.

Явление резкого возрастания амплитуды вынужденных колебаний на некоторой частоте, называемой резонансной (которая для малого затухания совпадает с частотой собственных колебаний w₀) называется резонансом .

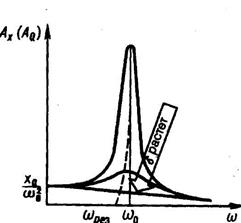
Рис.1.

Чем больше коэффициент затухания, тем ниже амплитуда при резонансе.

Амплитуда при резонансе A_res связана со статическим отклонением (при w стремящейся к нулю) через добротность Q:

A_res=QA_st, где .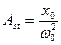

Чем выше добротность контура, тем выше амплитуда при резонансе.

Фазовая резонансные кривые построенные на основе (3), приведены на рис.2.

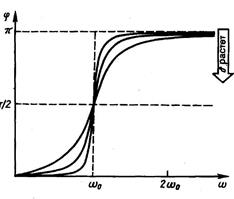
Рис.2.

Видно, что только в случае когда затухания нет (b=0), вынуждающая сила и колебания совпадают по фазе.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных, колебаний прибора. Так, радиотехника, прикладная акустика, оборудование, воспринимающее электрические колебания, основаны на явлении резонанс.