Двухмерное преобразование относительно произвольной точки.

P(x,y) – над которой выполняется преобразование

P₁(x₁,y₁)

Результирующее положение точки P’(x’,y’). Относительно начала координат мы знаем. Проще всего так:

1) Сдвинем начало координат в точку P₁(x₁,y₁).

2) Выполним все нужные действия над точкой P.

3) Вернёмся к исходной системе координат.

Сдвиг всей картинки на величину –x₁ и –y₁:

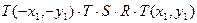
сдвиг действия возврат

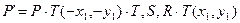
Есть отдельные сокращённые матрицы для сдвига, масштаба и поворота относительно любой точки. Смысл – сократить количество операций умножения.

Например.

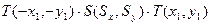– результат – это матрица размером 3х3.

Результат умножения таких матриц имеет вид:

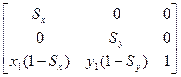
Пользоваться перемноженными матрицами можно, если используется не очень быстрая ЭВМ. Причём это касается в первую очередь видеосистемы (не успевает выполнить умножение за время регенерации кадров). Во всех остальных случаях пользоваться упрощёнными формулами не имеет смысла.

Очень часто применяется способ упрощения реализации поворота. От кадра к кадру угол меняется не более чем на 1 градус. В этом случае косинус близок к 1, то есть cos a »1, при a £ 1°:

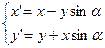
На каждом шаге погрешность очень маленькая, однако если количество оборотов достигнет двух и более, то погрешность может достигнуть веских величин, поэтому пройдя полный круг 360°, нужно вернуться к исходному положению точки, то есть погасить погрешность.