Кинематика и динамика вращательного движения
Если точка движется по окружности радиусом R, то ее положение в пространстве удобно характеризовать углом поворота 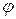 , отсчитываемым от некоторого направления. Например, на рисунке 5.2 угол
, отсчитываемым от некоторого направления. Например, на рисунке 5.2 угол 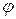 отсчитывается «против хода часовой стрелки» от положительного направления оси OX.
отсчитывается «против хода часовой стрелки» от положительного направления оси OX.
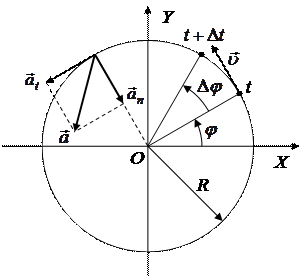
Рисунок 5.2 - Движение точки по окружности.
Быстроту вращения характеризует угловая скорость  - предел отношения приращения
- предел отношения приращения 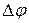 угла поворота к затраченному времени
угла поворота к затраченному времени 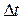 при условии, что
при условии, что 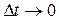 , то есть первая производная от угла поворота по времени:
, то есть первая производная от угла поворота по времени:
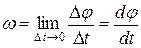 . (5.14)
. (5.14)
Быстроту изменения угловой скорости характеризует угловое ускорение 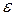 , равное
, равное
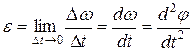 . (5.15)
. (5.15)
Обычная (линейная) скорость направлена по касательной к траектории и связана с угловой скоростью соотношением
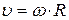 . (5.16)
. (5.16)
Ускорение 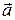 точки направлено под углом к траектории и является векторной суммой нормального (центростремительного) ускорения
точки направлено под углом к траектории и является векторной суммой нормального (центростремительного) ускорения 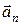 и тангенциального (касательного) ускорения
и тангенциального (касательного) ускорения 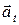 , модули которых таковы:
, модули которых таковы:
 . (5.17)
. (5.17)
Рассмотрим вращательное движение абсолютно твердого (недеформируемого) тела вокруг неподвижной оси OZ (на рисунке 5.3 перпендикулярна плоскости рисунка и направлена «на нас») под действием сил  , лежащих в плоскости, перпендикулярной оси OZ (силы или составляющие сил, параллельные оси OZ, очевидно, вызвать вращение тела не могут).
, лежащих в плоскости, перпендикулярной оси OZ (силы или составляющие сил, параллельные оси OZ, очевидно, вызвать вращение тела не могут).
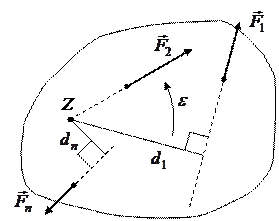
Рисунок 5.3 - Тело, вращающееся вокруг оси OZ под действием внешних сил.
Из второго закона Ньютона выводится основной закон динамики вращательного движения твердого тела с неподвижной осью вращения:
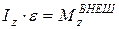 . (5.18)
. (5.18)
Он напоминает по форме сам второй закон Ньютона, но содержит другие величины. Сравним (5.18) и (5.9). Вместо проекции 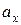 ускорения точки на ось OX в (5.18) входит угловое ускорение
ускорения точки на ось OX в (5.18) входит угловое ускорение 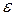 всех точек вращающегося тела. Входящая в (5.9) масса m есть мера инертности точки или поступательно движущегося протяженного тела. Вместо m в (5.18) входит мера инертности тела при вращательном движении - момент инерции тела относительно оси OZ, обозначенный
всех точек вращающегося тела. Входящая в (5.9) масса m есть мера инертности точки или поступательно движущегося протяженного тела. Вместо m в (5.18) входит мера инертности тела при вращательном движении - момент инерции тела относительно оси OZ, обозначенный 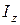 . Для материальной точки массой m, находящейся на расстоянии r от оси вращения,
. Для материальной точки массой m, находящейся на расстоянии r от оси вращения,
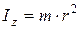 , (5.19)
, (5.19)
а для протяженного тела момент инерции равен сумме моментов инерции всех точек этого тела:
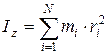 , (5.20)
, (5.20)
где i=1, 2, ... N - номер точки.
Наконец, в (5.9) внешнее воздействие на точку характеризовала проекция на ось OX равнодействующей силы 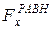 , а в (5.18) внешнее воздействие на вращающееся тело характеризует
, а в (5.18) внешнее воздействие на вращающееся тело характеризует 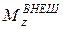 - суммарный момент относительно оси OZ действующих на тело внешних сил. Он равен алгебраической сумме моментов относительно оси OZ всех внешних сил, а каждый из этих моментов есть произведение силы на плечо d (кратчайшее расстояние от оси до линии действия силы):
- суммарный момент относительно оси OZ действующих на тело внешних сил. Он равен алгебраической сумме моментов относительно оси OZ всех внешних сил, а каждый из этих моментов есть произведение силы на плечо d (кратчайшее расстояние от оси до линии действия силы):
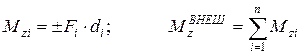 . (5.21)
. (5.21)
В формуле (5.21) в выражении для 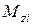 берется знак «+», если сила
берется знак «+», если сила 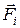 вращает тело «против хода часовой стрелки» (если смотреть навстречу оси OZ), и знак «-», если сила
вращает тело «против хода часовой стрелки» (если смотреть навстречу оси OZ), и знак «-», если сила 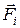 вызывает вращение во встречном направлении.
вызывает вращение во встречном направлении.
Например, для ситуации, представленной на рисунке 5.3, 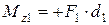 (сила
(сила 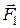 вращает тело «против хода часовой стрелки»), в то же время
вращает тело «против хода часовой стрелки»), в то же время 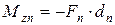 , а
, а 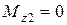 , так как линия действия силы
, так как линия действия силы 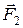 проходит через ось вращения, и ее плечо равно нулю.
проходит через ось вращения, и ее плечо равно нулю.
Зная момент инерции тела и момент внешних сил, учтя, что 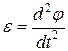 , решим уравнение (5.18) и найдем закон движения тела, то есть зависимость
, решим уравнение (5.18) и найдем закон движения тела, то есть зависимость 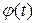 . Как и при решении аналогичного уравнения (5.10), для однозначного определения закона движения требуется информация о состоянии тела в некоторый момент. При вращательном движении эта информация сводится к данным об угле его поворота
. Как и при решении аналогичного уравнения (5.10), для однозначного определения закона движения требуется информация о состоянии тела в некоторый момент. При вращательном движении эта информация сводится к данным об угле его поворота 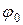 и угловой скорости
и угловой скорости 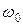 в некоторый момент времени
в некоторый момент времени 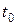 .
.
Дата добавления: 2020-10-25; просмотров: 596;











