Механической энергии. Превращения энергии

Поскольку движение и взаимодействие взаимосвязаны (взаимодействие определяет движение материальных объектов, а движение объектов, в свою очередь, влияет на их взаимодействие), то должна быть единая мера, характеризующая движение и взаимодействие материи.

Энергия и является единой скалярной количественной мерой различных форм движения и взаимодействия материи. Различным формам движения и взаимодействия соответствуют различные виды энергии: механическая, внутренняя, электромагнитная, ядерная и т.д. Простейшим видом энергии, соответствующим простейшей - механической - форме движения и взаимодействия материи, является механическая энергия.

Одним из наиболее важных законов всего естествознания является всеобщий закон сохранения энергии. Он утверждает, что энергия не возникает ниоткуда и не исчезает бесследно, а лишь переходит из одной формы в другую.

Закон сохранения механической энергии есть частный случай всеобщего закона сохранения энергии.

Полная механическая энергия материальной точки (частицы) и системы частиц складывается из двух частей. Первая составляющая энергии частицы обуславливается ее движением, называется кинетической энергией и вычисляется по формуле

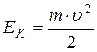, (6.11)

где m - масса частицы, - ее скорость.

Кинетическая энергия частицы изменяется, если при движении частицы на нее действует сила (силы), совершающая работу.

В простейшем случае, когда сила 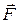постоянна по величине и по направлению, а траектория движения прямолинейна, то работа A, совершаемая этой силой при перемещении 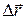, определяется по формуле

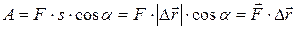, (6.12)

где s - пройденный путь, равный при прямолинейном движении модулю перемещения 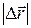, 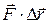- скалярное произведение векторов 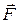и 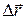, равное произведению модулей этих векторов на косинус угла между ними.

Работа может быть положительной, если угол острый ( 90°), отрицательной, если угол тупой (90° 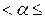180°), и может быть равна нулю если угол прямой ( =90°).

Можно доказать, что изменение кинетической энергии 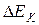частицы при ее перемещении из точки 1 в точку 2 равно сумме работ, совершенных всеми силами, действующими на эту частицу, при данном перемещении:

, (6.13)

где - кинетическая энергия частицы в начальной и в конечной точках, 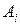- работа, совершенная силой 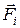(i=1, 2, ... n) при данном перемещении.

Кинетической энергией системы 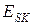из N частиц называется сумма кинетических энергий всех частиц системы. Ее изменение при любом изменении конфигурации системы, то есть произвольном перемещении частиц, равно суммарной работе 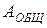, совершенной всеми силами, действующими на частицы системы, при их перемещениях:

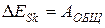. (6.14)

Второй составляющей механической энергии является энергия взаимодействия, называемая потенциальной энергией. В механике понятие потенциальной энергии может быть введено не для любых взаимодействий, а лишь для определенного их класса.

Пусть в каждой точке пространства, где может находиться частица, на нее в результате взаимодействия с другими телами действует сила, зависящая только от координат x, y, z частицы и, возможно, от времени t: . Тогда говорят, что частица находится в силовом поле взаимодействия с другими телами. Примеры: материальная точка, движущаяся в гравитационном поле Земли; электрон, движущийся в электростатическом поле неподвижного заряженного тела. В этих примерах сила, действующая на частицу, в каждой точке пространства от времени не зависит: 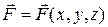. Такие поля называются стационарными.

Если же, например, электрон будет находиться в электрическом поле конденсатора, напряжение между обкладками которого изменяется, то в каждой точке пространства сила будет зависеть и от времени: . Такое поле называется нестационарным.

Далее ограничимся рассмотрением лишь стационарных силовых полей.

Сила, действующая на частицу, называется консервативной, а соответствующее поле – полем консервативной силы, если работа, совершаемая этой силой при перемещении частицы по произвольному замкнутому контуру, будет равна нулю.

К консервативным силам и соответствующим полям относятся сила всемирного тяготения и, в частности, сила тяжести (гравитационное поле), сила Кулона (электростатическое поле), сила упругости (поле сил, действующих на тело, прикрепленное к некоторой точке упругой связью).

Примерами неконсервативных сил являются сила трения, сила сопротивления среды движению тела.

Только для взаимодействий, которым соответствуют консервативные силы, может быть введено понятие потенциальной энергии.

Под потенциальной энергией 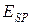механической системы понимается величина, убыль которой (разность начального и конечного значений) при произвольном изменении конфигурации системы (изменении положения частиц в пространстве) равна работе , совершаемой при этом всеми внутренними консервативными силами, действующими между частицами этой системы:

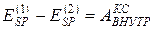, (6.15)

где 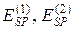- потенциальная энергия системы в начальной и конечной конфигурации.

Заметим, что убыль 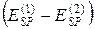равна с обратным знаком приращению (изменению) 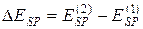потенциальной энергии и поэтому соотношение (6.15) можно записать в виде

. (6.16)

Такое определение потенциальной энергии системы частиц позволяет находить ее изменение при изменении конфигурации системы, но не само значение потенциальной энергии системы при заданной конфигурации. Поэтому во всех конкретных случаях уславливаются, при какой конфигурации системы (нулевой конфигурации) ее потенциальная энергия 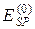принимается равной нулю ( 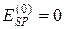). Тогда потенциальная энергия системы при любой ее конфигурации 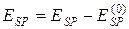, а из (6.15) следует, что

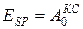, (6.17)

то есть потенциальная энергия системы частиц некоторой конфигурации равна работе 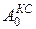, совершаемой внутренними консервативными силами при изменении конфигурации системы от данной до нулевой.

Потенциальная энергия тела, находящегося в однородном поле силы тяжести вблизи поверхности Земли, принимается равной нулю при нахождении тела на поверхности Земли. Тогда потенциальная энергия притяжения к Земле тела, находящегося на высоте h, равна работе силы тяжести 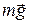, совершаемой при перемещении тела с этой высоты на поверхность Земли, то есть на расстояние h по вертикали:

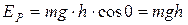. (6.18)

Потенциальная энергия тела, прикрепленного к фиксированной точке упругой связью (пружиной), принимается равной нулю при недеформированной связи. Тогда потенциальная энергия упруго деформированной (растянутой или сжатой на величину 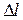) пружины с коэффициентом жесткости k равна

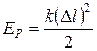. (6.19)

Потенциальная энергия гравитационного взаимодействия материальных точек и электростатического взаимодействия точечных зарядов принимается равной нулю, если эти точки (заряды) удалены на бесконечное расстояние друг от друга. Поэтому энергия гравитационного взаимодействия материальных точек массам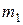и и , находящихся на расстоянии r друг от друга, равна работе силы всемирного тяготения 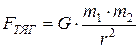, совершенной при изменении расстояния x между точками от x=r до :

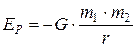. (6.20)

Из (6.20) следует, что потенциальная энергия гравитационного взаимодействия материальных точек при указанном выборе нулевой конфигурации (бесконечном удалении) оказывается отрицательной при размещении точек на конечном расстоянии друг от друга. Это связано с тем, что сила всемирного тяготения есть сила притяжения, и ее работа при удалении точек друг от друга отрицательна. Отрицательность потенциальной энергии означает, что при переходе этой системы из произвольной конфигурации в нулевую (при удалении точек с конечного расстояния на бесконечное) ее потенциальная энергия увеличивается.

Аналогично, потенциальная энергия электростатического взаимодействия точечных зарядов в вакууме равна

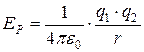(6.21)

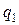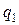и отрицательна для притягивающихся разноименных зарядов (знаки и различны) и положительна для отталкивающихся одноименных зарядов (знаки и одинаковы).

Полной механической энергией системы (механической энергией системы) 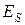называется сумма ее кинетической и потенциальной энергий

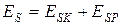. (6.22)

Из (6.22) следует, что изменение полной механической энергии складывается из изменения ее кинетической и потенциальной энергии

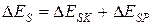. (6.23)

Подставим в формулу (6.33) формулы (6.14) и (6.16). В формуле (6.14) общую работу 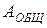всех сил, действующих на точки системы, представим как сумму работы сил, внешних по отношению к рассматриваемой системе, и работы внутренних сил, которая, в свою очередь, складывается из работы внутренних консервативных и неконсервативных сил, :

.

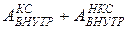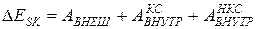После подстановки получим, что

. (6.24)

Для замкнутой системы 0. Если система к тому же консервативна, то есть в ней действуют только внутренние консервативные силы, то и =0. В этом случае уравнение (6.24) принимает вид 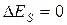, а это означает, что

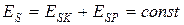. (6.25)

Уравнение (6.2) есть математическая запись закона сохранения механической энергии, который гласит: полная механическая энергия замкнутой консервативной системы постоянна, то есть не изменяется со временем.

Условие 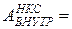0 выполняется, если в системе действуют и неконсервативные силы, но их работа равна нулю, как, например, при наличии сил трения покоя. В этом случае для замкнутой системы закон сохранения механической энергии также применим.

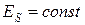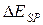Отметим, что при отдельные слагаемые механической энергии: кинетическая и потенциальная энергия, - не обязаны оставаться постоянными. Они могут изменяться, что сопровождается совершением работы консервативными внутренними силами , но изменения потенциальной и кинетической энергии и 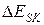равны по модулю и противоположны по знаку. Например, за счет совершения внутренними консервативными силами работы над частицами системы ее кинетическая энергия возрастет, но при этом на равную величину уменьшится ее потенциальная энергия.

Если же в системе совершают работу неконсервативные силы, то это обязательно сопровождается взаимными превращениями механической и иных видов энергии. Так, совершение работы неконсервативными силами трения скольжения или сопротивления среды обязательно сопровождается выделением тепла, то есть переходом части механической энергии во внутреннюю (тепловую) энергию. Неконсервативные силы, работа которых приводит к переходу механической энергии в тепловую, называются диссипативными, а сам процесс перехода механической энергии в тепловую - диссипацией механической энергии.

Есть множество неконсервативных сил, работа которых, напротив, ведет к увеличению механической энергии системы за счет иных видов энергии. Например, в результате химических реакций происходит взрыв снаряда; при этом осколки получают прибавку механической (кинетической) энергии за счет работы неконсервативной силы давления расширяющихся газов - продуктов взрыва. В этом случае посредством совершения работы неконсервативных сил произошел переход химической энергии в механическую. Схема взаимных превращений энергии при совершении работы консервативными и неконсервативными силами представлена на рисунке 6.3.

Таким образом, работа есть количественная мера превращения одних видов энергии в другие. Работа консервативных сил равна количеству потенциальной энергии, перешедшей в кинетическую или наоборот (общая механическая энергия при этом не изменяется), работа неконсервативных сил равна количеству механической энергии, перешедшей в другие виды энергии или наоборот.

Рисунок 6.3 - Схема превращений энергии.

Всеобщий закон сохранения энергии фактически есть закон неуничтожимости движения в природе, а закон сохранения механической энергии - закон неуничтожимости механического движения при определенных условиях. Изменение же механической энергии при невыполнении этих условий не означает уничтожения движения или его появления ниоткуда, а свидетельствует о превращении одних форм движения и взаимодействия материи в другие.

Обратим внимание на отличие обозначений бесконечно малых величин. Например, dx обозначает бесконечно малое приращение координаты, 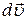- скорости, dE – энергии, а бесконечно малую работу обозначают 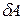. Это отличие имеет глубокий смысл. Координаты и скорость частицы, ее энергия и многие другие физические величины являются функциями состояния частицы (системы частиц), то есть определяются текущим состоянием частицы (системы частиц) и не зависят от того, какими были предшествующие состояния, и от того, каким способом частица (система) пришла в текущее состояние. Изменение такой величины можно представить как разность значений этой величины в конечном и начальном состояниях. Бесконечно малое изменение такой величины (функции состояния) называется полным дифференциалом и для величины X обозначается dX.

Такие же величины, как работа или количество теплоты, характеризуют не состояние системы, а способ, которым был реализован переход из одного состояния системы в другое. Например, говорить о наличии работы у системы частиц в каком-то заданном состоянии бессмысленно, но можно говорить о работе, совершенной силами, действующими на систему, при ее переходе из одного состояния в другое. Таким образом, не имеет смысла говорить и о разности значений такой величины в конечном и начальном состояниях. Бесконечно малое количество величины Y, не являющейся функцией состояния, обозначается .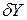

Отличительным признаком функций состояния является то, что их изменения в процессах, в которых система, выйдя из исходного состояния, в него же и возвращается, равны нулю. Механическое состояние системы частиц задается их координатами и скоростями. Поэтому, если в результате некоторого процесса механическая система возвращается в исходное состояние, то координаты и скорости всех частиц системы принимают первоначальные значения. Механическая энергия, как величина, зависящая только от координат и скоростей частиц, также примет исходное значение, то есть не изменится. В то же время работа, совершенная силами, действующими на частицы, будет отлична от нуля, причем ее значение может быть разным в зависимости от вида траекторий, описанных частицами системы.