Принцип суперпозиции в классической физике. Описание состояния механической системы. Принцип механического детерминизма. Динамические закономерности

Вернемся к вопросу о состоянии точки в некоторый момент времени, то есть о том, какой информацией о точке надо располагать, чтобы однозначно определить закон ее последующего движения. Для этого мы должны обратиться к динамике - разделу механики, изучающему движение во взаимосвязи с причинами, вызывающими это движение.

Для точки постоянной массы m, рассматриваемой относительно некоторой инерциальной системы отсчета OXYZ, справедлив второй закон Ньютона в виде (3.2):

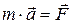. (5.7)

Если же на точку действуют несколько сил 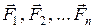, то ускорение 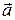точки есть векторная сумма ускорений 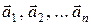, сообщаемых этой точке каждой из сил по отдельности. Последнее утверждение не следует из законов Ньютона, а представляет собой самостоятельный принцип (принцип суперпозиции), справедливость которого проверяется на опыте. В физике мы неоднократно встречаемся с различными проявлениями принципа суперпозиции (принципа наложения), являющегося одним из важнейших физических принципов.

В общем виде в классической физике принцип суперпозиции гласит, что результирующий эффект совокупности воздействий есть сумма эффектов, вызываемых каждым воздействием в отдельности, при условии, что эти воздействия не влияют друг на друга.

Применительно к задаче о движении точки последнее условие означает, что воздействие каждой из сил не меняет массу точки, а вызываемое этой силой движение не меняет свойств пространства и времени. В классической механике это действительно так, но при необходимости использовать для изучения движения специальную или общую теорию относительности эти условия не выполняются и принцип суперпозиции ускорений неприменим.

Точно так же известный принцип суперпозиции электрических и магнитных полей ( 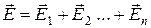- для напряженности электрического поля, 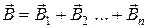- для индукции магнитного поля) выполняется, лишь если каждое из накладывающихся полей не изменяет свойств среды, в которой существует поле. Поэтому в классической электродинамике принцип суперпозиции полей справедлив, например, в вакууме и нарушается, например, в ферромагнитных средах, магнитная проницаемость которых не постоянна, а сама зависит от присутствия магнитного поля.

Таким образом, принцип суперпозиции является нестрогим, его применимость в каждом конкретном случае должна быть обоснована. В квантовой физике принцип суперпозиции получает дальнейшее развитие, о чем будет сказано ниже.

В классической механике ускорение, вызываемое каждой из сил 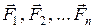, может быть найдено с помощью уравнения (5.7): 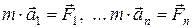, и, ввиду выполнимости принципа суперпозиции для ускорений, мы получаем, что

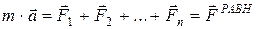, (5.8)

где 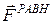- равнодействующая сила, равная для материальной точки векторной сумме всех сил, действующих на нее.

Силы, действующие на материальную точку, могут зависеть от ее положения относительно окружающих тел, то есть от координат точки: 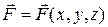- к ним относятся силы всемирного тяготения, упругости, Кулона. Постоянные силы, например, силы тяжести у поверхности Земли 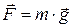можно рассматривать как частный случай таких сил. Существуют также силы, зависящие от скорости движения точки: 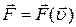, - такие, как сила сопротивления среды движению, сила Лоренца. Наконец, сила, действующая на тело, может явно зависеть от времени. Например, даже если точка неподвижна, но тела, с которыми оно взаимодействует, перемещаются, то силы гравитационного, кулоновского взаимодействий точки с этими телами зависят от времени. Вообще говоря, механические силы, действующие на точку, зависят от ее координат, скорости и времени: .

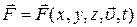Для простоты рассмотрим ситуацию, когда точка может двигаться только вдоль оси OX. Тогда, проецируя на ось OX векторные величины в уравнении (5.8), получаем

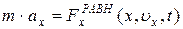, (5.9)

где 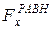- проекция на ось OX равнодействующей силы, которая, как было сказано выше, может быть постоянной, но может и зависеть от координаты x точки, проекции 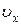ее скорости на ось OX и времени t.

Если учесть соотношение (5.6), то уравнение (5.9) принимает вид:

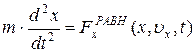. (5.10)

Уравнение второго закона Ньютона, записанное в виде (5.10), представляет собой дифференциальное уравнение второй степени относительно переменной x и называется уравнением движения точки.

Рассмотрим простейший случай, когда сила, действующая на точку массой m, постоянна, то есть 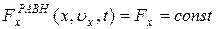. В таком случае решение уравнения (5.10) имеет вид:

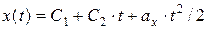, (5.11)

где 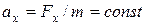- проекция на ось OX ускорения точки.

В справедливости решения (5.11) легко убедиться, подставив его в уравнение (5.10).

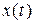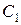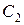Чтобы однозначно установить закон движения точки, необходимо определить значения констант интегрирования и . Для определения 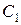достаточно знать начальную координату точки 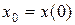. Действительно, полагая в (5.11) t=0, а 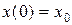, видим, что .

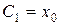Для определения 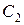продифференцируем (5.11) по времени, получим

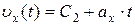, (5.12)

откуда ясно, что для нахождения 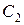достаточно знать проекцию на ось OX начальной скорости точки, то есть 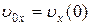. Действительно, полагая в (5.12) t=0 и 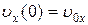, получаем, что .

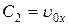Итак, закон движения точки под действием постоянной силы (закон равноускоренного движения) принимает вид

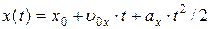, (5.13)

причем мы убедились, что для установления закона движения недостаточно знать массу точки и действующую на нее силу, но необходимо иметь дополнительную информацию, например, знать начальную координату и начальную скорость точки. Можно показать, что и при действии на точку массой m непостоянной силы для установления закона ее движения необходимо знать ее координату и скорость в некоторый момент времени, например, при t=0.

Мы пришли к выводу, что в классической механике состояние материальной точки заданной массы в любой момент времени характеризуют ее координаты и скорость. Иногда вместо скорости рассматривают импульс точки .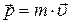

Из изложенного следует ряд важных выводов. Во-первых, если известны массы точек системы, их состояния, то есть координаты и скорости (или импульсы) в некоторый момент времени, и силы взаимодействия их друг с другом и внешними телами, то в принципе можно (хотя это может оказаться очень сложной задачей) определить сколь угодно точно и однозначно состояние системы точек, то есть их координаты и скорости, в любой последующий и предыдущий момент времени.

Принцип однозначной зависимости состояния механической системы в любой момент времени от ее состояния в другой момент называется принципом механического детерминизма (предопределенности) и является составной частью ньютоновской механистической парадигмы изучения мира.

Из идеи механического детерминизма следует, что возможно существо (устройство), называемое «демоном Паскаля», которое, располагая информацией о текущем состоянии мира (массах, координатах, скоростях тел) и неограниченными вычислительными возможностями, может сколь угодно точно предсказать состояние мира в будущем или, наоборот, установить, каким был мир в любой предыдущий момент.

Ньютоновская парадигма подразумевает взгляд на мир как на некоторый механизм (хотя и чрезвычайно сложный), который, будучи некогда приведен в действие, функционирует далее по предопределенному плану, в котором нет места случайностям и в принципе невозможно возникновение качественно иных форм движения и взаимодействия материи (например, биологической).

Великие открытия Ньютона позволили на научной основе анализировать и рассчитывать работу механических устройств, они объяснили законы движения планет (законы Кеплера) и стали основой небесной механики. Ньютон пытался перенести методы механики и в другие разделы физики, в частности, в оптику. Рассматривая свет как поток частиц (корпускул), подчиняющихся законам механики, он дал объяснение законам отражения и преломления света.

На длительный период в науке утвердилась механистическая картина мира, а в научной деятельности - механистическая парадигма. При решении какой-нибудь новой задачи исследователь, мыслящий в рамках этой парадигмы, рассуждал так: «Дайте мне информацию о массах тел, из которых состоит исследуемая система, их положениях и скоростях в некоторый момент времени, о силах их взаимодействия друг с другом и с другими телами, и я однозначно определю, что будет с этой системой в любой последующий момент времени и что было в любой предыдущий момент».

Такие закономерности, когда все последовательные состояния системы однозначно связаны друг с другом, в которых нет места случайности, называются динамическими закономерностями. Иначе говоря, динамическими называются такие закономерности, которые позволяют, зная состояние объекта исследования в некоторый момент времени и оказываемые на него воздействия, однозначно и сколь угодно точно определить его состояние в любой последующий и предыдущий момент времени. Как будет показано далее, область применения таких закономерностей – сравнительно простые неквантовые системы. В сложных и квантовых системах нельзя исключить роль случайностей и их поведение описывается вероятностными статистическими закономерностями.