Законы сохранения импульса и момента импульса

Импульсом материальной точки называется векторная величина , равная произведению массы m точки на ее скорость :

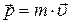, (6.1)

а импульсом системы материальных точек 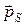- векторная сумма импульсов всех N точек этой системы:

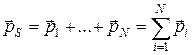. (6.2)

Система тел называется замкнутой, если на нее не действуют внешние силы.

Закон сохранения импульса гласит: импульс замкнутой системы постоянен, то есть не изменяется с течением времени.

Докажем это утверждение для упрощенного случая, когда система состоит лишь из двух материальных точек массами 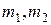, жестко связанных между собой, как в твердом теле, или могущих перемещаться относительно друг друга (рисунок 6.2). Внутренние силы взаимодействия точек системы друг с другом обозначим строчными буквами: 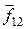(сила, действующая на точку номер 1 со стороны точки номер 2) и 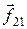. Силы, действующие со стороны внешних тел, обозначим заглавными буквами: .

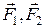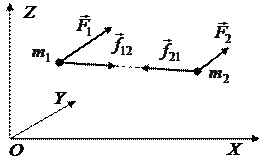
Рисунок 6.2 - Система материальных точек, рассматриваемая при выводе закона сохранения импульса.

Относительно инерциальной системы отсчета OXYZ для каждой точки запишем второй закон Ньютона в общем виде (3.1):

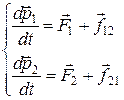(6.3)

Сложим эти равенства и учтем, что по третьему закону Ньютона 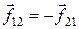, то есть сумма внутренних сил равна нулю: . Следовательно,

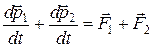или .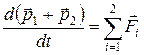

Но 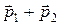есть импульс системы 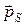, то есть

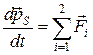. (6.4)

Если система замкнута, то, по определению, все внешние силы , следовательно, и их сумма

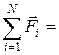0, (6.5)

и уравнение (6.4) принимает вид:

. (6.6)

Последнее равенство означает, что 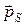не зависит от времени, то есть мы получаем математическую запись закона сохранения импульса (для системы из N точек):

или 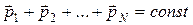. (6.7)

Отметим, что условие (6.5) выполняется и в случае, когда на точки системы внешние силы действуют, но они компенсируют друг друга. В этом случае закон сохранения импульса (6.7) также выполняется.

Подчеркнем, что при доказательстве закона сохранения импульса были использованы все три закона Ньютона, чтобы далее сопоставить это доказательство с другим, использующим свойства симметрии пространства.

Перейдем к закону сохранения момента импульса, особенно широко использующимся при изучении вращательного движения. Мы познакомимся с этим законом не в общем виде, а в частном случае, когда имеется система тел, могущих вращаться вокруг неподвижной оси OZ.

Как указывалось выше, быстроту вращения тела вокруг оси характеризует угловая скорость , а инертность тела при вращении вокруг оси характеризует момент инерции 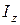относительно этой оси (формула (5.20) главы 5).

Моментом импульса тела 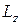относительно оси OZ называется произведение момента инерции тела относительно данной оси на угловую скорость вращения вокруг оси:

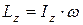. (6.8)

Момент импульса системы тел 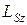относительно оси OZ есть алгебраическая сумма моментов импульсов относительно оси OZ всех тел системы:

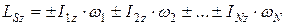. (6.9)

где моменты импульсов тел, вращающихся в одном направлении (по традиции – «против хода часовой стрелки», если смотреть навстречу оси OZ), берутся со знаком «+»", вращающихся в противоположном направлении – со знаком «-».

Закон сохранения момента импульса гласит: момент импульса относительно оси OZ замкнутой системы постоянен, то есть не изменяется с течением времени:

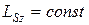. (6.10)

Этот закон выполняется и в том случае, когда на систему действуют внешние силы, но их суммарный момент относительно оси OZ (см. формулу (5.21) главы 5) равен нулю.