Кинематика материальной точки

КЛАССИЧЕСКАЯ МЕХАНИКА И КЛАССИЧЕСКАЯЭЛЕКТРОДИНАМИКА

Кинематика материальной точки

Если не рассматривать античный период и теологические концепции, то создание первой научной физической картины мира и формирование царствовавшей долгое время парадигмы связывают с именем гениального И. Ньютона.

Важнейшей частью научного наследия Ньютона является классическая (ньютоновская) механика, основы которой изложены в капитальном труде «Математические начала натуральной философии» (1687 г.). Ее главными составными частями являются:

- представление об абсолютном пространстве и абсолютном времени;

- механический принцип относительности (принцип относительности Галилея);

- введение понятий массы как меры инертных и гравитационных свойств материального тела и силы как меры механического взаимодействия тел;

- три закона Ньютона (основа классической динамики);

- закон всемирного тяготения, являющийся основой классической теории тяготения.

Концепции классической (ньютоновской) механика оказали на определенном этапе огромное влияние на методологию естествознания в целом.

В ней отсутствует даже предположение о взаимосвязи пространства, времени и материи, нет ограничений на возможную скорость движения тел.

Весь материальный мир по Ньютону предстает как набор вещественных тел: мелких, размерами которых можно пренебречь, то есть материальных точек, и крупных, протяженных, которые можно рассматривать как совокупность множества материальных точек. О возможности существования материи в виде поля Ньютон, по-видимому, не догадывался.

Взаимодействие тел в классической механике рассматривается как дальнодействие (см. подраздел 3.1), то есть как влияние тел друг на друга, осуществляемое мгновенно через разделяющее тела пространство без участия посредника, каковым по современным представлениям является поле.

В классической механике впервые пришлось столкнуться с понятием состояния тела (системы тел). Под состоянием тела (системы тел) понимается совокупность его свойств и отношений с окружающими телами, позволяющая описать его дальнейшее движение (развитие). Описать состояние материального объекта - значит дать тот минимальный объем информации о нем, который при условии, что известно, как на него воздействуют окружающие объекты, позволит прогнозировать его дальнейшее движение (развитие).

Важнейшим объектом изучения классической механики является материальная точка. Каким же необходимым набором сведений о ней нужно располагать в некоторый момент времени, чтобы иметь возможность определить (рассчитать) ее последующее движение?

Для ответа на этот вопрос вначале познакомимся с основами кинематики - раздела механики, занимающегося описанием движения, не затрагивая вопрос о причинах этого движения.

Основными способами описания положения точки в некоторый момент времени являются:

- координатный, когда указываются координаты точки в данный момент времени относительно выбранной системы координат (очень часто - координаты x, y, z относительно прямоугольной декартовской системы координат);

- векторный, когда указывается радиус-вектор 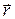точки, то есть вектор, соединяющий начало координат с точкой (см. рисунок 5.1).

При использовании декартовской системы координат OXYZ с единичными векторами 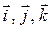, направленными по осям OX, OY, OZ, связь координат x, y, z точки с ее радиус-вектором такова:

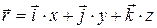. (5.1)

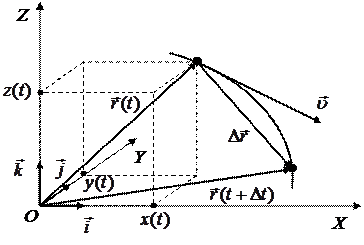
Рисунок 5.1 - Координатный и векторный способы описания положения и движения точки.

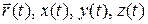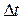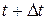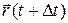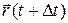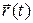На рисунке 5.1 - радиус-вектор и координаты точки в момент времени t. Если точка движется, то спустя время , то есть в момент времени , ее радиус-вектор будет иным, изменятся и координаты точки. Разность векторов и , то есть вектор, соединяющий положения точки в моменты t и 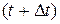, называется вектором перемещения: .

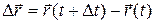Проекции вектора 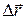на оси OX, OY, OZ (на рисунке 5.1 не показаны) равны приращениям соответствующих координат точки: 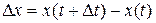, аналогично для .

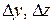Быстроту движения точки характеризует вектор скорости (мгновенной скорости) , равный пределу отношения приращения 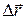радиус-вектора (то есть перемещения) ко времени 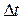, за которые произошло это приращение, при условии, что 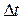стремится к нулю:

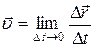. (5.2)

Как известно из математики, если величина y есть функция величины x, то предел 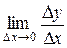, если он существует, называется производной от величины y по x и обозначается 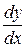. Следовательно, формула (5.2) может быть записана в виде:

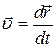, (5.3)

то есть мгновенная скорость есть первая производная от радиус-вектора точки по времени. Вообще, скорость изменения какой-либо величины есть первая производная по времени от данной величины.

Быстроту движения точки вдоль каждой из осей OX, OY, OZ характеризуют скалярные величины - проекции вектора скорости на данные оси, равные производным от соответствующих координат по времени:

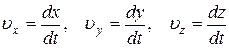. (5.4)

Быстроту изменения скорости характеризует вектор ускорения 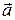, равный первой производной от скорости или второй производной от радиус-вектора точки по времени:

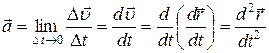, (5.5)

а быстроту изменения проекций 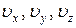скорости на координатные оси характеризуют соответствующие проекции ускорения:

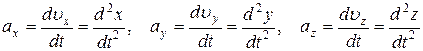. (5.6)

Описать движение точки означает установить, как радиус-вектор точки или ее координаты зависят от времени, то есть установить вид зависимост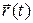и или 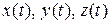. Если такая зависимость известна, то говорят, что задан закон движения точки.