Понятие симметрии. Симметрия кристаллов

Под симметрией (от греч. symmetria - соразмерность) в самом широком общенаучном плане понимается неизменность (инвариантность) каких-либо свойств объектов относительно некоторых преобразований (преобразований симметрии). Симметричными объектами могут быть предметы и их взаимодействия, процессы или описывающие их уравнения или относящиеся к ним законы, геометрические фигуры, живые организмы и так далее.

Примерами преобразований симметрии являются сдвиги в пространстве, вращения, зеркальное отражение в пространстве, сдвиги и обращение во времени, зарядовое сопряжение (замена частиц на античастицы), а также их комбинации.

Понятие симметрии вначале стало широко применяться в минералогии и кристаллографии при изучении внешней формы и внутреннего строения кристаллов. У кристаллов симметричной бывает, во-первых, их внешняя форма, которая может воспроизводиться при поворотах, отражениях, инверсии (симметрии относительно точки), инверсионных поворотах (комбинации поворота с инверсией). Множество различных преобразований, в результате которых кристалл данной формы самосовмещается, называется точечной группой симметрии этого кристалла. Например, для кристалла берилла в виде прямой призмы с основаниями - правильными шестиугольниками (рисунок 6.1а) элементами точечной группы симметрии являются повороты на угол 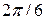вокруг оси OZ (оси симметрии 6-го порядка), поворота на угол 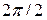вокруг осей OX и OY и любых других осей, проходящих через центры противоположных боковых граней или середины противоположных ребер (осей симметрии 2-го порядка), зеркальное отражение относительно плоскости OXY или шести вертикальных плоскостей, проходящих через ось OZ и противоположные вершины или середины противоположных ребер шестиугольных оснований. Элементом точечной группы симметрии этой призмы является также инверсия относительно центра O, то есть перенос каждой точки кристалла по линии, проходящей через эту точку и центр О, в положение, равноудаленное от центра О, но лежащее по другую сторону от него.

Во-вторых, у кристаллов симметрично строение кристаллической решетки, то есть пространственное расположение частиц (атомов, ионов, молекул), из которых состоит данный кристалл. Зачастую вся кристаллическая решетка может быть получена переносом небольшой группы атомов, образующих так называемую элементарную ячейку, вдоль осей OX, OY, OZ (не обязательно взаимно перпендикулярных) с шагом a по оси OX, шагом b по оси OY, шагом c по оси OZ. На рисунке 6.1б показана элементарная объемно-центрированная кубическая ячейка кристалла железа при t< 912ºC ( 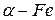), представляющая собой куб, в центре которого находится еще один атом железа. Вся кристаллическая решетка железа может быть построена переносом двух выделенных черным цветом атомов вдоль перпендикулярных осей OX, OY, OZ с равным для всех осей шагом a.

Рисунок 6.1 - Внешняя форма кристалла берилла (а) и элементарная ячейка кристалла железа при температуре до 912ºС (б).

Множество преобразований, в результате которых некоторая решетка совмещается сама с собой, называется ее пространственной группой симметрии. Кроме элементов, образующих точечную группу, характеризующую симметрию внешней формы данного кристалла, пространственная группа симметрии содержит также переносы с шагами 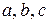вдоль осей OX, OY, OZ. В некоторых более сложных кристаллах возможно самосовмещение кристаллической решетки при ее переносе вдоль некоторой оси с одновременным поворотом вокруг оси, то есть при винтовом переносе.

Использование понятия симметрии в кристаллографии позволило установить и классифицировать все возможные внешние формы и типы кристаллических решеток, установить взаимосвязь внешней формы и внутреннего строения. Но симметричными оказались не только геометрические, но и физические свойства кристаллов. Кристаллы, как правило, анизотропны, то есть их физические свойства (упругость, диэлектрическая и магнитная проницаемости, показатель преломления и т.д.) различны для разных направлений. Эти свойства также обладают симметрией, то есть оказываются неизменными при определенных поворотах кристалла, смене направления воздействия и т.д. Связь симметрии физических свойств кристалла с симметрией его кристаллической решетки и внешней формы широко используется в науке и технике. Эта связь может быть весьма сложной, но доказано, что симметрия любого физического свойства кристалла (то есть количество элементов в группе преобразований, оставляющих данное свойство неизменным) не может быть ниже симметрии его внешней формы (принцип Неймана).

Не менее продуктивным оказалось применение методов, связанных с исследованием симметрии объектов, в других областях физики.

К важным последствиям привело установление того, что симметрия пространства и времени тесно связана с законами сохранения в механике.

Известны три закона сохранения в механике: законы сохранения импульса, момента импульса, а также закон сохранения механической энергии.