Гипергеометрическое распределение
Пусть множество из 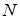 элементов содержит
элементов содержит 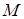 элементов, обладающих некоторым свойством, и
элементов, обладающих некоторым свойством, и 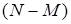 элементов, которые ими не обладают. Из этого множества наудачу выбирается
элементов, которые ими не обладают. Из этого множества наудачу выбирается 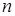 элементов (делается безвозвратная выборка объема
элементов (делается безвозвратная выборка объема 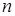 ). Какова вероятность того, что среди выбранных
). Какова вероятность того, что среди выбранных 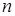 элементов окажется ровно
элементов окажется ровно 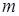 элементов с рассматриваемым свойством?
элементов с рассматриваемым свойством?
Эта задача играет большую роль в ряде областей практического применения вероятностных моделей в демографии, статистике населения, статистическом контроле качества продукции и др.
Очевидно, что элементарные исходы данного опыта представляют собой сочетания без повторений из 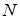 элементов по
элементов по 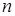 . Число таких исходов
. Число таких исходов 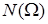 =
= 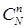 . Каждая выборка, входящая в событие
. Каждая выборка, входящая в событие 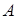 ={среди отобранных
={среди отобранных 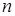 элементов ровно
элементов ровно 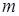 обладают рассматриваемым свойством}, состоит из двух частей: 1)
обладают рассматриваемым свойством}, состоит из двух частей: 1) 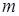 с рассматриваемым свойством и 2) (
с рассматриваемым свойством и 2) ( 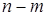 ) без этого свойства. Все такие выборки можно получить следующим образом. Сначала составим части выборок из элементов с рассматриваемым свойством; число таких частей
) без этого свойства. Все такие выборки можно получить следующим образом. Сначала составим части выборок из элементов с рассматриваемым свойством; число таких частей 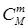 . Затем отдельно составим части выборок из элементов без этого свойства; число таких частей
. Затем отдельно составим части выборок из элементов без этого свойства; число таких частей 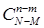 . Объединение любой части выборки из элементов с рассматриваемым свойством с любой частью выборки из элементов без этого свойства дает полный набор элементов, принадлежащих событию
. Объединение любой части выборки из элементов с рассматриваемым свойством с любой частью выборки из элементов без этого свойства дает полный набор элементов, принадлежащих событию 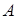 . Следовательно,
. Следовательно, 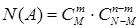 и по формуле классической вероятности
и по формуле классической вероятности
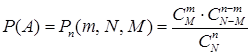 . (5)
. (5)
Здесь и далее предполагается, что 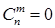 при
при 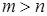 . Набор чисел
. Набор чисел 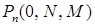 ,
, 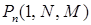 … называют гипергеометрическим распределением.
… называют гипергеометрическим распределением.
Пример. Из 20 деталей, среди которых четыре – нестандартные, наудачу выбираются шесть. Какова вероятность, что среди них не будет нестандартных?
◄ Исходное множество деталей состоит из двух частей: из 16 стандартных и из 4 нестандартных деталей. Элементарные исходы данного опыта – сочетания по 6 деталей из 20. Рассматриваемое событие: 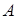 ={среди отобранных шести деталей нет нестандартных}. Применяя формулу (5), будем иметь
={среди отобранных шести деталей нет нестандартных}. Применяя формулу (5), будем иметь 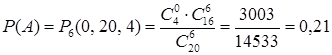 . ►
. ►
Дата добавления: 2016-07-27; просмотров: 2019;











