Характеристики рассеивания
Дисперсией случайной величины X называется неотрицательное число 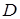 [Х]
[Х] 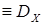 , определяемое формулой
, определяемое формулой
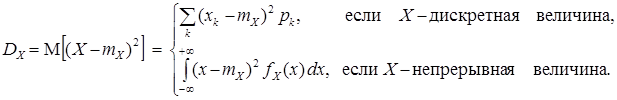 (4)
(4)
Неотрицательное число 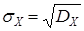
 называется среднеквадратичным отклонением (сокращенно с. к. о.) случайной величины X. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. (Величину
называется среднеквадратичным отклонением (сокращенно с. к. о.) случайной величины X. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. (Величину 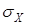 иногда называют стандартным отклонением.) Если величина X =const (т. е. X не случайна), то
иногда называют стандартным отклонением.) Если величина X =const (т. е. X не случайна), то 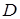 [
[ 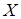 ] = 0.
] = 0.
Свойства дисперсии:
a. Дисперсия любой случайной величины 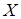 неотрицательна, причем
неотрицательна, причем 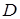 [X] = 0 тогда и только тогда, когда
[X] = 0 тогда и только тогда, когда 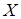 – постоянная;
– постоянная;
b. Если 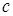 – постоянная, то
– постоянная, то
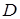 [
[ 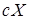 ] =
] = 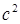
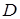 [
[ 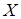 ];
];
c. Если случайные величины X и Y независимы, то
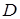 [
[ 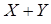 ] =
] = 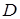 [
[ 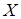 ]+
]+ 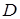 [
[ 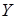 ].
].
Случайная величина X называется центрированной (обозначается 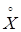 ), если mX = 0. Случайная величина X называется стандартизованной, если
), если mX = 0. Случайная величина X называется стандартизованной, если
mX = 0 и 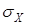 =1 (т. е. начало отсчета находится в
=1 (т. е. начало отсчета находится в 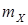 , а единицей измерения величины является
, а единицей измерения величины является 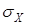 ).
).
Начальным моментомm-го порядка( 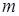 = 0, 1, 2, ...) распределенияслучайной величины X называется действительное число
= 0, 1, 2, ...) распределенияслучайной величины X называется действительное число 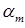 , определяемое по формуле
, определяемое по формуле
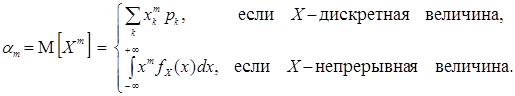 (5)
(5)
Центральным моментомm-го порядка распределения случайной величины X называется число 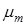 , определяемое по формуле
, определяемое по формуле
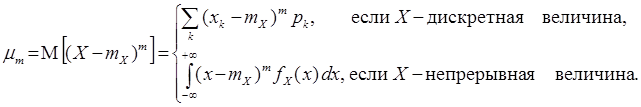 (6)
(6)
Из определений моментов, в частности, следует, что
a0 = 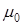 = 1, mX = a1 , DХ =
= 1, mX = a1 , DХ = 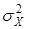 =
= 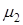 = a2 -
= a2 - 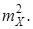
Отметим еще две важные характеристики распределения, связанные с моментами высшего порядка:
· коэффициент асимметрии или «скошенности» распределения
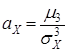 , (7)
, (7)
· коэффициент эксцесса или «островершинности» распределения
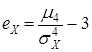 . (8)
. (8)
Квантилью порядка 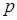 распределения случайной величины X непрерывного типа называется действительное число
распределения случайной величины X непрерывного типа называется действительное число 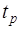 , удовлетворяющее уравнению
, удовлетворяющее уравнению
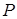 {Х <
{Х < 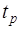 } =
} = 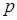 . (9)
. (9)
Дата добавления: 2016-07-27; просмотров: 2583;











