Понятие случайной величины
Случайной величиной 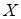 называется числовая функция X = X (
называется числовая функция X = X ( 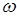 ) от элементарных событий
) от элементарных событий 
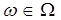 . Таким образом, случайная величина определена на множестве элементарных исходов
. Таким образом, случайная величина определена на множестве элементарных исходов 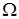 и в зависимости от случая принимает разные числовые значения. Из этого определения случайных величин следует, что на них распространяются все правила действий с обычными функциями: их можно складывать, вычитать, перемножать и т. д.
и в зависимости от случая принимает разные числовые значения. Из этого определения случайных величин следует, что на них распространяются все правила действий с обычными функциями: их можно складывать, вычитать, перемножать и т. д.
Случайные величины принято обозначать прописными буквами латинского алфавита X, Y, Z,…, а их возможные значения - соответствующими малыми буквами.
Пример. Пусть множество элементарных исходов состоит из шести равновероятных исходов 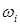 ,
, 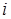 = 1, 2,…, 6. Определим на этом множестве следующие случайные величины:
= 1, 2,…, 6. Определим на этом множестве следующие случайные величины:
а) Х ( 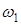 ) = 1, Х (
) = 1, Х ( 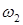 ) = 2, Х (
) = 2, Х (  ) = 3, Х (
) = 3, Х ( 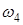 ) = 4, Х (
) = 4, Х ( 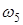 ) = 5, Х (
) = 5, Х ( 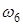 ) = 6;
) = 6;
б) Y ( 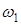 ) = 1, Y (
) = 1, Y ( 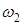 ) = 0, Y (
) = 0, Y (  ) = 1, Y (
) = 1, Y ( 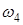 ) = 0, Y (
) = 0, Y ( 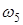 ) = 1, Y (
) = 1, Y ( 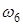 ) = 0;
) = 0;
в) Z ( 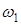 ) = -1, Z (
) = -1, Z ( 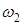 ) = 1, Z (
) = 1, Z (  ) = -1, Z (
) = -1, Z ( 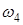 ) = 1, Z (
) = 1, Z ( 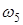 ) = -1, Z (
) = -1, Z ( 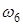 ) = 1.
) = 1.
Сумма случайных величин X и Y дает новую случайную величину W, которая определяется из равенства
W ( 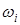 ) = X (
) = X ( 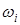 ) + Y (
) + Y ( 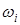 ).
).
Следовательно,
W ( 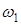 ) = 2, W (
) = 2, W ( 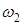 ) = 2, W (
) = 2, W (  ) = 4, W (
) = 4, W ( 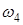 ) = 4, W (
) = 4, W ( 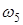 ) = 6, W (
) = 6, W ( 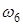 ) = 6.
) = 6.
Произведение случайных величин Y и Z даст другую новую случайную величину V, определенную равенством
V ( 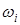 ) = Y (
) = Y ( 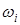 ) · Z (
) · Z ( 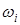 ).
).
Из этого равенства следует
V ( 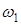 ) = -1, V (
) = -1, V ( 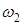 ) = 0, V (
) = 0, V (  ) = -1, V (
) = -1, V ( 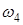 ) = 0, V (
) = 0, V ( 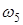 ) = -1, V (
) = -1, V ( 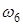 ) = 0.
) = 0.
Пример. В схеме независимых испытаний Бернулли множество 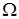 состоит из элементарных событий (цепочек)
состоит из элементарных событий (цепочек) 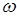 = (
= ( 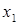 ,
, 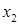 , …,
, …, 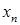 ), где
), где 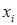 = 1, если при
= 1, если при 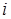 -м испытании произошел успех, и
-м испытании произошел успех, и 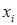 = 0 в случае неудачи. Случайная величина X = X (
= 0 в случае неудачи. Случайная величина X = X ( 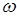 ) =
) = 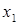 +
+ 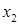 +…+
+…+ 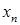 равна числу успехов при
равна числу успехов при 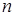 испытаниях в схеме Бернулли.
испытаниях в схеме Бернулли.
Любую константу С можно рассматривать как частный случай случайной величины X = X ( 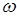 ) ≡ С. Такие случайные величины называются вырожденными. Простейшими случайными величинами, отличными от вырожденных, являются индикаторы. С каждым событием
) ≡ С. Такие случайные величины называются вырожденными. Простейшими случайными величинами, отличными от вырожденных, являются индикаторы. С каждым событием  можно связать случайную величину
можно связать случайную величину
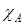 =
= 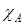 (
( 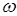 ) = 1, если
) = 1, если 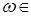 А;
А; 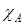 =
= 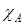 (
( 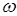 ) = 0, если
) = 0, если 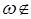 А,
А,
называемую индикаторомсобытия А. Индикаторы удовлетворяют следующим легко проверяемым свойствам:
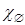 = 0,
= 0, 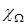 = 1,
= 1, 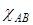 =
= 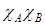 ,
, 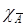 = 1 –
= 1 – 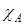 .
.
Если события 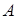 и
и 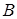 несовместны, то
несовместны, то
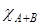 =
= 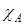 +
+ 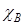 .
.
Пусть 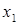 <
< 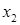 < … <
< … <  – всевозможные значения случайной величины X. Из определения случайной величины и основных свойств вероятностей можно найти вероятности, с которыми случайная величина X принимает свои возможные значения
– всевозможные значения случайной величины X. Из определения случайной величины и основных свойств вероятностей можно найти вероятности, с которыми случайная величина X принимает свои возможные значения 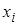 ,
, 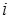 = 1, 2,…,
= 1, 2,…, 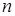 . Обозначим через
. Обозначим через 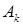 событие, состоящее из всех тех элементарных исходов
событие, состоящее из всех тех элементарных исходов 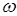 , для которых X (
, для которых X ( 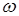 ) принимает значение
) принимает значение 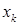 :
: 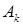 = {
= { 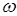 | X (
| X ( 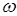 ) =
) = 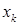 }. Тогда вероятность того, что X примет значение
}. Тогда вероятность того, что X примет значение 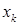 , равна
, равна 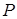 {
{ 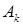 }. В зависимости от значений
}. В зависимости от значений 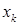 событие
событие 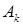 может оказаться невозможным, состоять из одного исхода, из двух и даже из всего множества элементарных исходов.
может оказаться невозможным, состоять из одного исхода, из двух и даже из всего множества элементарных исходов.
В вышеприведенном примере для случайной величины 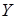 нетрудно получить следующие вероятности ее числовых значений:
нетрудно получить следующие вероятности ее числовых значений:
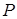 {
{ 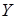 = 0} = 1/2,
= 0} = 1/2, 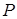 {
{ 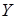 = 1} = 1/2,
= 1} = 1/2,
а для величины W
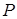 {W = 2} = 1/3,
{W = 2} = 1/3, 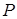 {W = 4} = 1/3,
{W = 4} = 1/3, 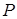 {W = 6} = 1/3.
{W = 6} = 1/3.
Дата добавления: 2016-07-27; просмотров: 1918;











