Предельные теоремы в схеме Бернулли

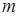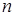В приложениях часто приходится вычислять вероятности различных событий, связанных с числом успехов в испытаниях Бернулли при больших значениях 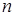. При больших значениях 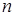и 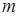вычисления по формуле (16) становятся затруднительными. Так, если 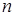=100 и 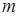=50. то для вычисления 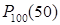необходимо найт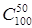и и 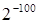. Трудности возникают и в том случае, когда приходится суммировать вероятности 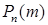, а также при малых значениях 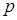или .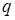

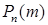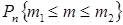В вышеперечисленных случаях мы имеем дело с ситуацией, когда точные выражения оказываются бесполезны для практических расчетов, и возникает необходимость в приближенных формулах. Ниже рассматриваются три предельные теоремы для вероятностей и при .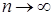

Теорема Пуассона. Если 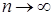, а вероятность «успеха» 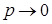, причем, причем 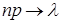, то

.

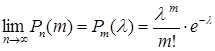Из этого предельного равенства следует, что при больших 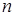и малых 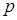(обычно достаточно 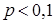) можно воспользоваться приближенной формулой

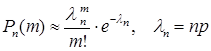. (17)

Пример. Вероятность того, что изделие, сошедшее с конвейера, является бракованным, равна 0,015. Найти вероятность того, что среди 100 случайно отобранных изделий, не будет бракованных.

◄ По формуле Бернулли будет иметь 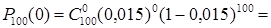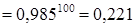. Если использовать приближенную формулу (17) при 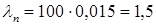, то получим ►

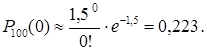Формулой (17) можно пользоваться не только при малых значениях вероятности 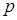, но и тогда, когда мало значение 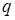. В последнем случае пуассоновским приближением можно воспользоваться для числа наступления «неудач».