Интегральная теорема Муавра-Лапласа

Пусть 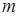– число успехов в 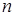независимых испытаниях по схеме Бернулли. Тогда при достаточно больших значениях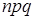

.

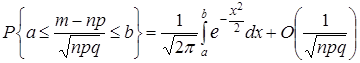Приближенная формула

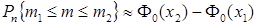, где

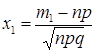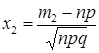, , (19)

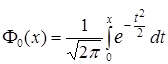– функция Лапласа или интеграл вероятности

(значения последнего интеграла табулированы и приводятся в справочниках по теории вероятностей), дает хорошее приближение, когда 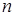достаточно велико, а 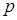и 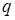не очень близки к нулю (обычно достаточно выполнение условия 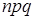>20).

Пример. Две симметричные монеты подбрасываются 1000 раз. Найти приближенное значение вероятности того, что число выпадений двух гербов заключено между 236 и 264.

◄ По условию задачи 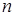=1000, 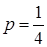(т. к. всего элементарных исходов этого опыта 4, а событию {ГГ} благоприятствует один из них), 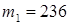, 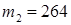. Имеем 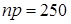, , 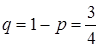, , 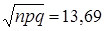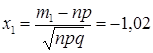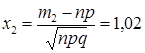. По формуле (19) находим . ►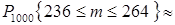

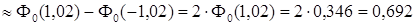С помощью формулы (19) можно оценить вероятность 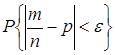отклонения 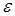( 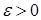) частоты 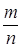в 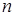испытаниях Бернулли от вероятности успеха :

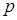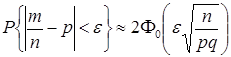. (20)

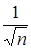Из этой формулы вытекает, что отклонения частоты от вероятности имеют порядок , т. е.

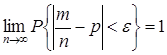(теорема Бернулли). (21)

Для оценки вероятности того, что отклонение частоты 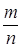в схеме Бернулли от вероятности 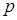не больше , можно использовать неравенство

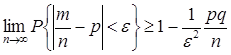. (22)

Если задать сколь угодно малое число 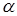( 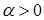) и найти 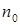из равенства 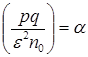, то согласно (22) при 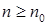с вероятностью, не меньшей 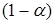, частота 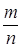будет находиться в пределах .

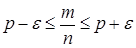Пример. Сколько раз надо подбросить симметричную монету, чтобы с вероятностью 0,90 частота 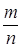отличалась от 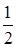(вероятности выпадения герба) не более чем на 0,01?

◄ Используем формулу (20). По условию задачи 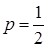, , 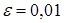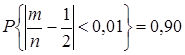. Тогда 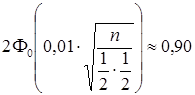, откуда 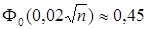. Используя таблицу значений функции 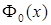, получаем 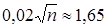и, следовательно, . ►

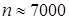Лекция №14