Случайные величины в общей схеме
В случае произвольного вероятностного пространства случайной величиной 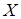 называется такая функцияX = X (
называется такая функцияX = X ( 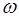 ) от элементарных исходов
) от элементарных исходов 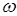 , для которой при любом численном значении
, для которой при любом численном значении 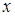 неравенство {X ≤
неравенство {X ≤ 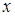 } является событием. Вероятность этого события
} является событием. Вероятность этого события 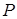 {X ≤
{X ≤ 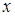 } называется функцией распределения. Таким образом, функция распределения
} называется функцией распределения. Таким образом, функция распределения 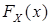 случайной величины X определяется формулой
случайной величины X определяется формулой
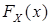 =
= 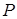 {X ≤ x}. (3)
{X ≤ x}. (3)
Функция распределения обладает следующими свойствами:
a) 0 ≤ 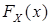 ≤ l, –
≤ l, – 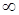 < x <
< x < 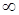 ;
;
b) FX (– 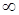 ) = 0, FX (+
) = 0, FX (+ 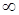 ) = 1;
) = 1;
c) 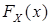 - неубывающая функция на всей оси;
- неубывающая функция на всей оси;
d) 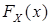 непрерывна справа, т. е.
непрерывна справа, т. е. 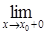
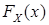 =
= 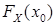 .
.
Вероятность попадания случайной величины X на произвольный интервал действительной оси ( 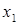 ,
, 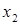 ] определяется формулой
] определяется формулой
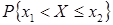 =
= 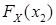 –
– 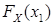 . (4)
. (4)
Различают случайные величины дискретного типа и случайные величины непрерывного типа. Определение дискретных случайных величин и их законов распределения дано выше. Зная закон распределения таких величин, можно вычислить функцию распределения, представляющую собой, в силу определения (3), функцию накопленных вероятностей:
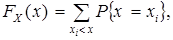 (5)
(5)
где суммирование распространяется на все значения индекса 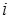 , для которых
, для которых 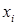 <
< 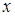 . Это ступенчатая функция, которая принимает постоянное значение на любом интервале, не содержащем значений случайной величины
. Это ступенчатая функция, которая принимает постоянное значение на любом интервале, не содержащем значений случайной величины 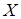 . Ее точки разрыва – это ее возможные значения
. Ее точки разрыва – это ее возможные значения 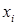 , а скачки в точках разрыва – соответствующие вероятности
, а скачки в точках разрыва – соответствующие вероятности 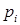 .
.
Случайная величина Х называется случайной величиной непрерывного типа, если существует такая неотрицательная функция 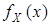 , называемая плотностью распределения вероятностей, что при всех
, называемая плотностью распределения вероятностей, что при всех 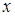
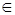 R
R
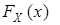 =
= 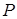 {X ≤
{X ≤ 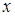 } =
} = 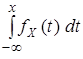 . (6)
. (6)
Плотность распределения вероятностей обладает следующими свойствами:
a) 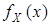 ≥ 0, –
≥ 0, – 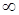 < x <
< x < 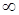 ;
;
b)  =l (условие нормировки);
=l (условие нормировки);
c) 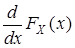 =
= 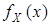 в точках непрерывности функции
в точках непрерывности функции 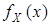 .
.
Функция распределения непрерывной случайной величины 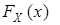 является непрерывной монотонно возрастающей функцией на всей оси, причем
является непрерывной монотонно возрастающей функцией на всей оси, причем
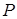 {Х =
{Х = 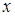 } =
} =  = 0 при всех x
= 0 при всех x 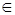 R.
R.
Это значит, что вероятность «попасть в точку» для непрерывной случайной величины, равна нулю.
Если Х - непрерывная случайная величина, то вероятность ее попадания на интервал ( 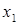 ,
, 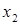 ] может быть вычислена как через функцию распределения по формуле (4), так и через плотность распределения вероятностей:
] может быть вычислена как через функцию распределения по формуле (4), так и через плотность распределения вероятностей:
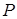 {
{ 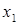 < Х ≤
< Х ≤ 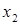 } =
} = 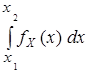 . (7)
. (7)
Пример. Функция 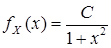 является плотностью распределения некоторой непрерывной случайной величины. Найти: значение нормирующей постоянной
является плотностью распределения некоторой непрерывной случайной величины. Найти: значение нормирующей постоянной 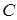 , функцию распределения, вероятность
, функцию распределения, вероятность
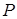 {0< Х ≤ 1}.
{0< Х ≤ 1}.
◄ Постоянную 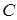 находим из условия нормировки плотности распределения
находим из условия нормировки плотности распределения  =l:
=l: 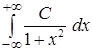 =
= 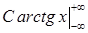 =
= 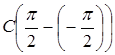 =
= 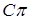
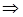
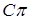 =1
=1 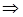
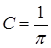 . Итак,
. Итак, 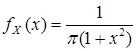 .
.
Функцию распределения найдем исходя из определяющей ее формулы (6): 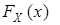 =
= 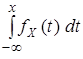 =
=  =
= 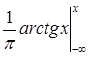 =
=  .
.
По формуле (7) находим искомую вероятность 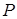 {0< Х ≤ 1}:
{0< Х ≤ 1}:
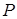 {0< Х ≤ 1} =
{0< Х ≤ 1} = 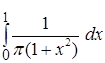 =
= 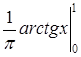 =
= 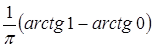 =
= 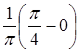 =
=
= 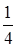 . Этот результат можно получить и с помощью функции распределения по формуле(4):
. Этот результат можно получить и с помощью функции распределения по формуле(4): 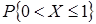 =
=  –
– 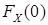 =
= 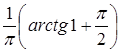 –
–
– 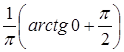 =
= 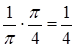 . ►
. ►
Дата добавления: 2016-07-27; просмотров: 2590;











