Формула полной вероятности
Пусть { 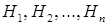 } – разбиение множества элементарных исходов для данного опыта, интерпретируемое как совокупность гипотез по отношению к интересующему нас событию
} – разбиение множества элементарных исходов для данного опыта, интерпретируемое как совокупность гипотез по отношению к интересующему нас событию  . Пусть опыт проведен, и стало известно, что событие
. Пусть опыт проведен, и стало известно, что событие  осуществилось, Какова апостериорная(послеопытная) вероятность наступления гипотезы
осуществилось, Какова апостериорная(послеопытная) вероятность наступления гипотезы 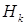 при условии, что событие
при условии, что событие  имело место? Ответ дается формулой Байеса:
имело место? Ответ дается формулой Байеса:
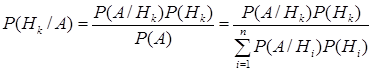 , (14)
, (14)
которая является следствием формулы полной вероятности (13).
Формулу Байеса иногда называют формулой гипотез. Она позволяет «переоценить» вероятность каждой из гипотез после поступления новой информации относительно наступления тех или иных наблюдаемых событий. Формула Байеса может служить также для принятия решений в тех случаях, когда гипотезы 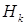 непосредственно не наблюдаемы, хотя априорные вероятности
непосредственно не наблюдаемы, хотя априорные вероятности 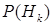 и соответствующие условные вероятности
и соответствующие условные вероятности 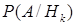 ,
, 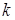 =1, 2, …,
=1, 2, …, 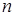 известны из дополнительных опытов.
известны из дополнительных опытов.
Пример. В условиях предыдущего примера случайно выбранное из партии изделие было признано дефектным. Какова вероятность того, что на самом деле изделие годно?
◄ В обозначениях предыдущего примера требуется найти 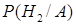 (апостериорную условную вероятность гипотезы
(апостериорную условную вероятность гипотезы 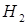 ). По формуле Байеса имеем
). По формуле Байеса имеем 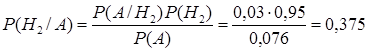 . Таким образом, апостериорная условная вероятность того, что изделие на самом деле годное, если известно, что оно было признано дефектным, существенно меньше априорной вероятности гипотезы
. Таким образом, апостериорная условная вероятность того, что изделие на самом деле годное, если известно, что оно было признано дефектным, существенно меньше априорной вероятности гипотезы 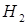 , что явилось следствием поступившей информации. ►
, что явилось следствием поступившей информации. ►
Пример. Из урны, содержащей 4 белых и 9 черных шаров, один шар неизвестного цвета был утерян. Какова вероятность того, что шар, извлеченный из урны после утери, окажется белым? Какова вероятность того, что утерян черный шар, если после утери извлечен белый шар?
◄ Нас интересует событие  ={шар, извлеченный из оставшихся шаров, белый}. Выберем следующие гипотезы:
={шар, извлеченный из оставшихся шаров, белый}. Выберем следующие гипотезы: 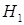 ={утерян белый шар},
={утерян белый шар}, 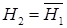 ={утерян черный шар}. В силу формулы классической вероятности
={утерян черный шар}. В силу формулы классической вероятности 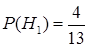 ,
, 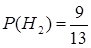 ,
, 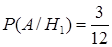 ,
, 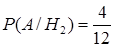 . По формуле полной
. По формуле полной 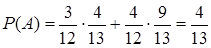 . Отметим, что вероятность извлечения белого шара из урны до утери также равна
. Отметим, что вероятность извлечения белого шара из урны до утери также равна 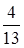 . Для нахождения апостериорной условной вероятности гипотезы
. Для нахождения апостериорной условной вероятности гипотезы 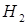
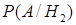 используем формулу Байеса:
используем формулу Байеса: 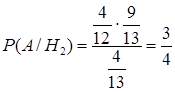 .►
.►
Дата добавления: 2016-07-27; просмотров: 4863;











