Формула полной вероятности
Пусть 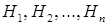 – наблюдаемые события для данного опыта, причем система множеств {
– наблюдаемые события для данного опыта, причем система множеств { 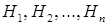 } образует разбиение множества элементарных исходов
} образует разбиение множества элементарных исходов 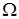 этого опыта, т. е. выполняются следующие условия:
этого опыта, т. е. выполняются следующие условия: 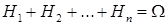 ,
, 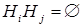 при любых
при любых 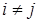 ,
, 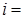 1, 2, …,
1, 2, …, 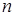 . Для любого наблюдаемого в опыте события
. Для любого наблюдаемого в опыте события  имеет место следующая формула (формула полной вероятности):
имеет место следующая формула (формула полной вероятности):
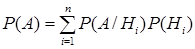 . (13)
. (13)
События 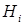 принято называтьгипотезами по отношению к событию
принято называтьгипотезами по отношению к событию  . Безусловные вероятности
. Безусловные вероятности 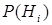 , для которых должно выполняться равенство
, для которых должно выполняться равенство 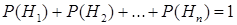 , трактуются как априорные(доопытные) вероятности гипотез. Для вычисления вероятности интересующего нас события по формуле (13) важно удачно подобрать набор гипотез. Если зависимость события
, трактуются как априорные(доопытные) вероятности гипотез. Для вычисления вероятности интересующего нас события по формуле (13) важно удачно подобрать набор гипотез. Если зависимость события  от гипотез
от гипотез 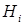 неясна и условные вероятности
неясна и условные вероятности 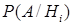 не могут быть просто вычислены, то такое разбиение не принесет практической пользы при решении задачи.
не могут быть просто вычислены, то такое разбиение не принесет практической пользы при решении задачи.
Пример. Партия изделий, среди которых 5% дефектных, поступила на проверку. Схема проверки такова, что с вероятностью 0,95 обнаруживается дефект (если он есть) и существует ненулевая вероятность 0,03 того, что годное изделие будет признано дефектным. Найти вероятность того, что случайно выбранное из партии изделие будет признано дефектным.
◄ Нас интересует событие  ={случайно выбранное изделие признано дефектным}. С этим событием тесно связаны две гипотезы:
={случайно выбранное изделие признано дефектным}. С этим событием тесно связаны две гипотезы: 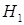 ={поступившее на проверку изделие дефектно},
={поступившее на проверку изделие дефектно}, 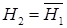 ={поступившее на проверку изделие годно}. Безусловные априорные вероятности этих гипотез равны
={поступившее на проверку изделие годно}. Безусловные априорные вероятности этих гипотез равны 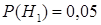 ,
, 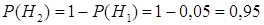 . Условные вероятности заданы в условии задачи:
. Условные вероятности заданы в условии задачи: 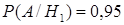 ,
, 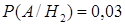 . По формуле полной вероятности получаем
. По формуле полной вероятности получаем 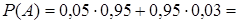
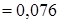 . ►
. ►
Дата добавления: 2016-07-27; просмотров: 3251;











