Аксиоматическое определение вероятности.

Пусть W – пространство элементарных событий, U – 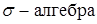событий. Вероятностью называется числовая функция 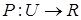, удовлетворяющая следующим трем аксиомам.

А1. 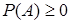для любого события A Î U.

А2. .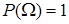

А3. Если события A₁, A₂, … из U попарно не пересекаются, то

P(A₁ + A₂ + …) = P(A₁) + P(A₂ ) + ….

Эта аксиома называется аксиомой s - адитивности.

Т.о., свойства классической вероятности 1)–3) из п.1.4. при аксиоматическом введении вероятности просто постулируются в качестве аксиом А1–А3. Аксиома А3 верна и для конечного числа событий (см. формулу (1.2)), которая называется аксиомой адитивности. Нетрудно доказать свойства 3)–8) из п. 1.4, исходя из этих аксиом. Заметим, что теорема сложения вероятностей для несовместных событий при аксиоматическом подходе постулируется как аксиома s - адитивности.

Определение. Вероятностным пространством называется тройка (W,U, P).

В дальнейшем подразумевается, что все события и вероятности рассматриваются в рамках некоторого вероятностного пространства (W,U, P).

При аксиоматическом подходе к понятию события и вероятности преодолеваются все недостатки классического, геометрического и статистического определений вероятности и аксиоматическое определение вероятности обобщает эти вероятности. Этот подход был введен выдающимся русским математиком А.Н. Колмогоровым в первой половине 20 века и является базовым понятием современной теории вероятностей.

Задача. В качестве W рассмотрим произвольное конечное множество из n элементов w₁, w₂, …, w_n. U – множество всех подмножеств W. Проверьте условия U1– U3 для множества U.

Вероятность определим по следующей схеме. Определим 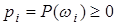, 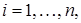так, чтобы 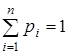. Тогда для любого события А определяем вероятность 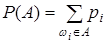. Проверьте выполнение аксиом А1– А3 для множества Р.