Независимость событий

Понятие условной вероятности позволяет в свою очередь ввести в математической модели понятие независимости. Будем считать, что событие 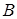не зависит от события , если выполняется равенство

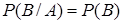. (5)

Если 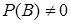, то из равенств (74) и (5) следует, что 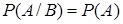, т. е. независимость является взаимным свойством: если 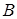не зависит от события , то и не зависит от события 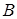. Более удобным определением независимости по сравнению с (5) является следующее.

События и 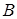называются независимыми, если

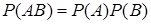. (6)

События 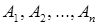называются взаимно независимыми (или независимыми в совокупности, или просто независимыми), если для любого набора из 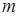событий ( 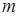=2, 3, …, 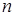) выполняется равенство

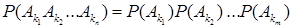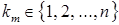, . (7)

Если (7) выполняется только при 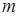=2, то события называютпопарнонезависимыми. Отметим, что из попарной независимости не следует независимость в совокупности.

Формулы (6) и (7) позволяют выделять независимые события в тех случаях, когда построена формализованная вероятностная модель случайного опыта и вероятности всех рассматриваемых событий определены. Однако далеко не всегда события, независимые в таком теоретико-вероятностном смысле, являются независимыми и в реальности. На практике в любых сомнительных случаях обычно стараются принять меры для объективной проверки гипотезы о независимости событий, основываясь на теоретико-вероятностной независимости, введенной равенствами (6) и (7), с причинной независимостью реальных событий. Решение подобных задач, основанное на применении методов проверки статистических гипотез, рассматривается в математической статистике.

Пример. В группе 25 студентов. Из них 10 человек курят, 13 носят очки, а 8 и курят и носят очки. Наудачу выбирается один студент. События: ={выбранный студент курит}, 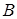={выбранный студент носит очки}. Установить, зависимы или нет события и .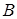

◄ Так как 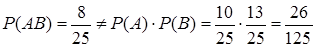, т. е. условие (6) независимости не выполняется, делаем вывод, что события и 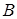зависимы.

Необходимо отметить, что полученный вывод справедлив лишь для данного частного эксперимента, и следует остерегаться распространять его на всех студентов вообще. Хотя гипотеза о зависимости между курением и состоянием зрения кажется разумной, для ее подтверждения необходимо было бы провести статистическое обследование всех студентов на определенной территории, которое включало бы проверку зрения у каждого и регистрацию длительности и интенсивности курения для тех, кто курит. Полученные статистические данные позволили бы на основе определенного критерия подтвердить либо отвергнуть наличие статистической зависимости между курением и состоянием зрения в той группе населения, которую составляют студенты. ►