Условные вероятности.
Аксиоматически определенную выше вероятность можно назвать безусловной вероятностью, подчеркивая этим, что она не зависит ни от каких дополнительных условий, кроме фиксированного комплекса условий 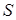 , которым характеризуется опыт.
, которым характеризуется опыт.
Пусть в опыте, соответствующему некоторому комплексу условий, могут произойти случайные события  и
и 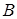 . Допустим также, что стало известно, что осуществилось событие
. Допустим также, что стало известно, что осуществилось событие  . Эта новая информация равносильна дополнительному условию, накладываемому на опыт и адекватному осуществлению события
. Эта новая информация равносильна дополнительному условию, накладываемому на опыт и адекватному осуществлению события  . В изменившемся комплексе условий опыта изменится и вероятностное распределение на его поле событий.
. В изменившемся комплексе условий опыта изменится и вероятностное распределение на его поле событий.
Пусть 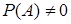 . Условная вероятность
. Условная вероятность 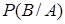 наступления события
наступления события 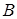 при условии, что событие
при условии, что событие  произошло в результате данного опыта, определяется следующей аксиомой:
произошло в результате данного опыта, определяется следующей аксиомой:
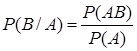 . (4)
. (4)
Условную вероятность 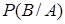 для краткости называют «вероятность события
для краткости называют «вероятность события 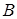 при условии
при условии  ». При
». При 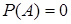 условная вероятность
условная вероятность 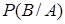 не определена.
не определена.
Пример. При бросании правильной игральной кости стало известно, что выпало четное число очков. Какова вероятность того, что выпала: а) двойка; б) пятерка?
◄ Исходное множество элементарных исходов для данного опыта 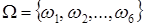 , где
, где 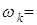 {число выпавших очков равно
{число выпавших очков равно 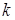 }, содержит
}, содержит 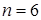 исходов. Три из них благоприятствуют событию
исходов. Три из них благоприятствуют событию  ={выпало четное число очков}, один исход благоприятствует событию
={выпало четное число очков}, один исход благоприятствует событию 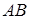 , где
, где 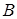 ={выпала двойка}. Число исходов, благоприятствующих событию
={выпала двойка}. Число исходов, благоприятствующих событию 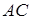 , где
, где 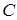 ={выпала пятерка}, равно нулю. По формуле (4) получаем:
={выпала пятерка}, равно нулю. По формуле (4) получаем: 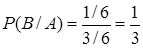 ,
, 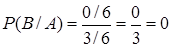 . ►
. ►
На практике для вычисления условной вероятности 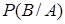 часто применяется метод вспомогательного эксперимента, при котором формулируется новый опыт, соответствующий комплексу условий
часто применяется метод вспомогательного эксперимента, при котором формулируется новый опыт, соответствующий комплексу условий 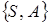 . В этом новом комплексе условий получают соответствующее ему множество элементарных исходов
. В этом новом комплексе условий получают соответствующее ему множество элементарных исходов 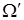 . Безусловная вероятность осуществления события
. Безусловная вероятность осуществления события 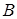 в этом новом опыте и принимается за условную вероятность
в этом новом опыте и принимается за условную вероятность 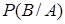 . Этот метод обычно применяется в тех случаях, когда вероятностное пространство для вспомогательного опыта строится проще, чем для исходного.
. Этот метод обычно применяется в тех случаях, когда вероятностное пространство для вспомогательного опыта строится проще, чем для исходного.
Пример. В условиях предыдущего примера новым множеством исходов будет 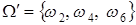 . Один из этих исходов благоприятствует событию
. Один из этих исходов благоприятствует событию 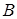 ={выпала двойка}, событию же
={выпала двойка}, событию же 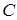 ={выпала пятерка} – ни один. По формуле классической вероятности получаем
={выпала пятерка} – ни один. По формуле классической вероятности получаем 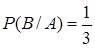 ,
, 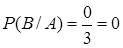 .
.
Дата добавления: 2016-07-27; просмотров: 2468;











