Оценка существенности коэффициента регрессии и уравнения регрессии

Параметры уравнения регрессии представляют собой лишь оценку реальных параметров связи в генеральной совокупности. Поэтому найдя по эмпирическим данным параметры уравнения регрессии, определяют их среднюю ошибку μ_a и с заданной вероятностью пределы, в которых эти параметры могут находиться. Затем параметры проверяют на существенность (значимость) путем сопоставления их значений со средней ошибкой. Это соотношение обозначают t.

t_a = a / μ_a .

Если значение t_a >3 при большом числе наблюдений, или t_факт > t_табл при n <30, параметр считается значимым.

Для приведенного примера ( 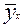= 1,16 +0,547 x , см. стр.102-103) определим t_факт для коэффициента регрессии а₁ по формуле:

t_a1 = 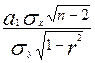= = 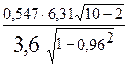= 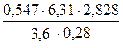(9,761/1,008)= 9,683.

Так как t_факт > t_табл (9,683 > 2,306), можно сделать вывод о значимости коэффициента регрессии а₁= 0.547.

Наряду с проверкой значимости отдельных параметров осуществляется проверка значимости уравнения регрессии в целом, то есть проверка адекватности модели. Эта задача решается путем расчета F-критерия Фишера и сопоставления его с табличным (критическим).

F-критерий Фишера представляет собой отношение факторной дисперсии к остаточной дисперсии, каждая из которых рассчитана на одну степень свободы:

F = ,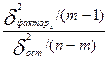

где m – число параметров в уравнении регрессии;

(m-1) – число степеней свободы для факторной дисперсии (теоретических значений y);

n - число наблюдений;

(n-m) - число степеней свободы для остаточной дисперсии.

Часто вместо числа параметров уравнения регрессии m принимается число коэффициентов регрессии k, которое на единицу меньше m, то есть k = m-1. А отношение дисперсий можно заменить корреляционным отношением или коэффициентом детерминации r². Тогда формула критерия Фишера будет иметь вид:

.

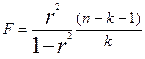Расчетное F сопоставляется с табличным, определяемым для числа степеней свободы ύ₁ = m-1 и ύ₂ =n-m и заданного уровня значимости α. Табличное F приводится в учебниках [16, Приложение 8]. Если F_расч > F_табл, уравнение значимо.

Проверим на значимость уравнение регрессии 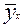= 1,16 +0,547 x, для которого r =0,96, n= 10, m=2:

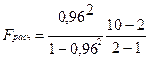= 0,9216/0,0784*8 = 94.

F_табл для α = 0, 05, ύ₁= 1, ύ₂ = 8 равно 5,32. Так как F_расч > F_табл , уравнение регрессии значимо, то есть зависимость между о выпуском продукции (x) и расходом условного топлива (y) в тоннах (графы 1 и 2 таблицы 2.2) реальна.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. В чем состоит отличие между корреляционной и функциональной связью?

2. Какие показатели используют для измерения степени тесноты связи между качественными признаками?

3. Как оценить существенность линейного коэффициента корреляции?

4. Если в случае линейной зависимости между признаками 60 % вариации результативного признака объясняется влиянием факторного признака, чему будет равна величина коэффициента корреляции?

5. Какая существует связь между линейным коэффициентом корреляции и коэффициентом регрессии?

6. В чем состоит значение уравнения регрессии?

7. Что характеризуют параметры уравнения регрессии?

8. Как осуществить прогноз значений результативного признака, опираясь на использование для этой цели уравнения регрессии?

9. Какое значение имеет расчет индекса корреляции?

10. Способы расчета средней квадратической ошибки уравнения, ее роль в оценке надежности уравнения регрессии.

11. Как измерить долю общей вариации результативного признака, которая объясняется влиянием вариации факторного признака?

ТЕСТЫ

1.В каких пределах изменяется парный коэффициент корреляции?

a) 0 ≤ p_xy ≤ 1;

b) – 1 ≤ p_xy ≤ 1;

c) – 1 ≤ p_xy≤ 0;

d) 0≤ p_xy≤ 10

2.В каких пределах именяется множественный коэффициент корреляции?

а) 0 ≤ R ≤ 1;

б)– 1 ≤ R ≤ 1;

в) -1 ≤ R ≤ 10;

г) -10 ≤ R ≤ 10

3.Коэффициент детерминации между x и y характеризует:

а) долю дисперсии y, обусловленную влиянием не входящих в модель факторов;

б) долю дисперсии y, обусловленную влиянием x;

в) долю дисперсии x, обусловленную влиянием не входящих в модель факторов;

г) направление зависимости между x и y.

4. Парный коэффициент корреляции между факторами равен 1.Это означает:

а) наличие нелинейной функциональной связи;

б) отсутствие связи;

в) наличие функциональной связи;

г) отрицательную связь.

5. На основании 20 наблюдений выяснено, что выборочная доля дисперсии случайной величины y, вызванной вариацией x, составит 64 %. Чему равен выборочный парный коэффициент корреляции? :

а) 0,64;

б) 0,36;

в) 0,8;

г)0,8 или – 0,8.

6. Уравнение регрессии имеет вид 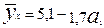. На сколько единиц своего измерения в среднем изменится y при увеличении x на одну единицу своего измерения:

а) увеличится на 1,7;

б) не изменится;

в) уменьшится на 1,7;

г)увеличится на 3,4.

7. Согласно методу наименьших квадратов в качестве оценок параметров β₀ и β₁, следует использовать такие значения b₀ и b₁,которые минимизируют сумму квадратов отклонений:

а) фактических значений зависимой переменной от ее среднего значения;

б) фактических значений объясняемой переменной от ее среднего значения;

в) расчетных значений зависимой переменной от ее среднего значения;

г) фактических значений зависимой переменной от ее расчетных значений.

8. Какой коэффициент в среднем указывает в среднем процент изменения результативного показателя y при увеличении аргумента x на 1 %:

а) β - коэффициент;

б) коэффициент эластичности;

в) коэффициент детерминации;

г) коэффициент регрессии.

9. Какая из следующих формул минимизируется в методе наименьших квадратов:

а) ;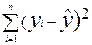

б) ;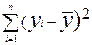

в) ;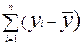

г) .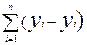

10. Дайте классификацию связей по аналитическому выражению:

а) обратная;

б) линейная;

в) функциональная.

11.Какой коэффициент характеризует связь между y и x:

а) парный;

б) частный;

в) множественный.

12. Признаком значении линейного коэффициента корреляции между y и x можно признать существенной:

а) 0,35;

б) 0,24;

в) 0,67.

13.Дайте интерпретацию коэффициента регрессии а:

а) на сколько в среднем изменится y при изменении x на единицу собственного измерения;

б) доля вариации y, обусловленная вариацией x;

в) на сколько в среднем изменится y при изменении x на 1 %.

Тема 2.2.