Идеал, факторкольцо.

Подкольцо M кольца K называется левым идеалом, если для любого a из K и b из M произведение a*b принадлежит M. Подкольцо M кольца K называется правым идеалом, если для любого a из K и b из M произведение b*a принадлежит M. Подкольцо M кольца K называется двусторонним идеалом, если M является и правым и левым идеалом. Двусторонний идеал часто называют идеалом, опуская слово «двусторонний».

Роль идеалов в теории колец во многом аналогична роли нормальных делителей в теории групп.

Рассмотрим множество смежных классов кольца K относительно идеала M относительно операции +. Относительно операции сложения множество смежных классов образуют абелевую группу (факторгруппу). При перемножении смежных классов a+M и b+M получим множество элементов, которые содержатся в смежном классе a*b+M. Таким образом, на множестве смежных классов вводится операция умножения. Относительно операции умножения, множество всех смежных классов образует полугруппу. Легко проверить, что дистрибутивность выполняется. Следовательно, множество смежных классов, относительно введенных операций сложения и умножения, образует кольцо, которое называют факторкольцом и обозначают K/M.

Кольцо вычетов.

В кольце целых чисел Z обозначим через (p) множество чисел кратных p. Легко проверить, что (p) образует идеал. Факторкольцо Z/(p) содержит p элементов вида {i+(p)}, где i=0,1,…,p-1. Смежный класс {i+(p)} для краткости обозначают i. Операции над классами эквивалентны обычным операциям сложения и умножения над остатками от деления на p (над вычетами). Поэтому, факторкольцо называют кольцом вычетов и обозначают.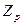

Теорема 3.3. Кольцо вычетов 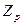является полем тогда и только тогда, когда p – простое число.

Доказательство. Кольцо вычетов 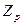не содержит делителей нуля тогда и только тогда, когда p - простое число. Конечное коммутативное кольцо без делителей нуля является полем.