Кольцо, подкольцо, идеал, факторкольцо.

Кольцо

Алгебра K с двумя бинарными операциями + и * называется кольцом, если выполняются условия

I. Множество K относительно операции + является абелевой группой.

II. Множество K относительно операции * образует полугруппу.

III. Операции связаны законами дистрибутивности, т.е. (a+b)*c=a*c+b*c и a*(b+c)=a*b+a*c.

Нейтральный элемент относительно сложения в кольце называют нулем и обозначают 0.

Свойство 3.1. a*0=0*a=0

Доказательство. a*0=a*(0+0)=a*0+a*0, откуда a*0=0. Аналогично, 0*a=0.

Если операция умножения в кольце коммутативна, то кольцо называется коммутативным.

Если множество ненулевых элементов кольца образуют группу относительно операции умножения, то кольцо называется телом. Коммутативное тело называется полем.

Подмножество M называется подкольцом (подтелом, подполем), если относительно операций + и * M образует кольцо (тело, поле).

Свойство 3.2. Для того чтобы подмножество M являлось подкольцом необходимо и достаточно, чтобы для любых a и b их сумма a+b, произведение a*b, и обратный (по сложению) –a, лежали в M.

Для того чтобы M являлось подтелом (подполем) требуется, чтобы с каждым ненулевым элементом a в M содержится и a^-1.

Примеры колец.

Имеется ряд стандартных конструкций колец на основе заданного кольца K.

Кольцо матриц

Пусть K – кольцо. Обозначим через 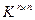множество всех квадратных матриц порядка n с элементами из кольца K. На множестве матриц определим операцию сложения C=A+B, 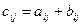и операцию умножения U=AB, 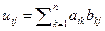. Относительно введенных операций множество матриц образует кольцо.

Кольцо многочленов

Обозначим через K(x) множество многочленов с коэффициентами из кольца K. На множестве этих многочленов можно определить операции сложения и умножения многочленов. Кольцо многочленов коммутативно если исходное кольцо коммутативно.