Область целостности

Рассмотрим вопрос, когда кольцо K можно вложить в некоторое поле (т.е. оно изоморфно некоторому кольцу в поле). Ясно, что необходимым условием является коммутативность кольца.

Элементы a,b из K, отличные от нуля и произведение которых равно 0, называются делителями нуля. В не коммутативном кольце различают левый и правый делители нуля, а, именно, если ab=0, то a – левый делитель, а b – правый делитель нуля.

Свойство 3.3. Тело не содержит делителей нуля.

Доказательство. Действительно, из 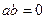, 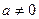вытекает .

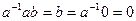Коммутативное кольцо без делителей нуля называется областью целостности.

Теорема 3.1. Конечное коммутативное кольцо K без делителей нуля является полем.

Доказательство. Пусть 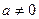. Рассмотрим последовательность 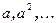степеней элемента a. Число различных элементов последовательности конечно, и, значит, найдутся в ней одинаковые элементы, например, с номерами k и j ( 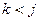, 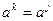). Но тогда, для любого b из K справедливо 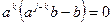, и, следовательно (т.к. нет делителей нуля ), 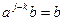. Элемент 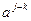является нейтральным относительно умножения. Если j-k>1, то 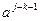- обратный элемент к a. Если j-k=1, то a является обратным сам к себе. Теорема доказана.

В общем случае, область целостности полем не является, например, кольцо целых чисел.

Поле частных

Теорема 3.2. Область целостности можно вложить в поле частных.

Доказательство. Пусть K- область целостности. Положим 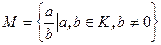. На множестве M введем бинарное отношение 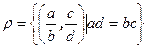. Это отношение рефлексивно ( 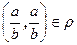), симметрично ( 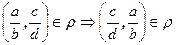) и транзитивно ( 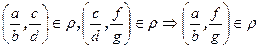), и, значит, является отношением эквивалентности. Множество M распадается на семейство не пересекающихся классов эквивалентности, которое обозначают 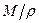. На множестве M определим операциисложения 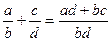и умножения 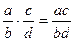. Пусть 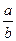принадлежит классу эквивалентности 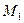, , 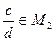, , 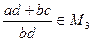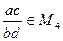тогда 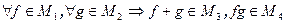(доказать самостоятельно). Таким образом, на множестве 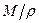определены операции сложения и умножения. Легко убедиться, что эти операции удовлетворяют аксиомам поля. Поле 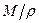называется полем частных. Подкольцо этого поля, состоящее из классов эквивалентности с представителями вида 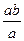, изоморфно K. Теорема доказана.

Примером поля частных является поле рациональных чисел.