Нормальный закон распределения
Определение:Непрерывная случайная величина Х имеетнормальный закон распределения (закон Гаусса), если ее плотность распределения имеет вид:
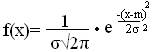 ,
,
где m=M(X), σ2=D(X), σ>0.
Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис.7)
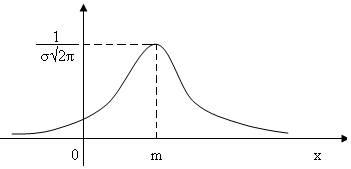 Нормальная кривая симметрична относительно прямой х=m, имеет максимум в т. х=а, равный
Нормальная кривая симметрична относительно прямой х=m, имеет максимум в т. х=а, равный 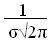 .
.
рис.7
Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф (х) по формуле:
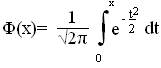
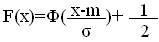 ,
,
где - функция Лапласа.
Замечание:Функция Ф(х) является нечетной (Ф(-х)=-Ф(х)), кроме того, при х>5 можно считать Ф(х) ≈1/2.
График функции распределения F(x) изображен на рис. 8
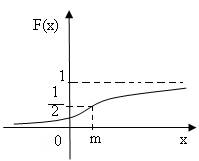 рис.8
рис.8
Вероятность того, что случайная величина Х примет значения, принадлежащие интервалу (a;b) вычисляются по формуле:
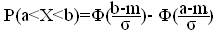
Вероятность того, что абсолютная величина отклонения меньше положительного числа δ вычисляется по формуле:
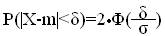
В частности, при m=0 справедливо равенство:
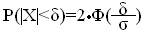
«Правило трех сигм»
Если случайная величина Х имеет нормальный закон распределения с параметрами m и σ, то практически достоверно, что ее значение заключены в интервале (a-3σ; a+3σ), т.к.
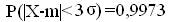
Задача №3. Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а)плотность распределения вероятностей f(x); б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
Решение: По условию m=32, σ2=16, следовательно, σ=4, тогда
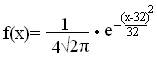 а)
а)
б) Воспользуемся формулой:
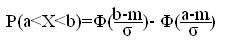
Подставив a=28, b=38, m=32, σ=4, получим
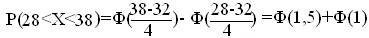
По таблице значений функции Ф(х) находим Ф(1,5)=0,4332, Ф(1)=0,3413.
Итак, искомая вероятность:
P(28<X<38)= 0,4332+0,3413=0,7745.
Дата добавления: 2016-07-18; просмотров: 2580;











