НОРМАЛЬНЫЙ (ГАУССОВСКИЙ) ЗАКОН РАСПРЕДЕЛЕНИЯ

Определение. Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

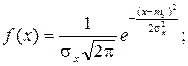
Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

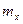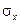Можно легко показать, что параметры и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.

Найдем функцию распределения F(x).

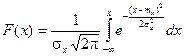
График плотности нормального распределения называется нормальной кривойили кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.

4) Найдем экстремум функции.

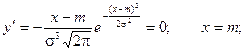
Т.к. при y’ > 0 при x < m и y’ < 0 при x > m , то в точке х = т функция имеет максимум, равный .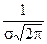

5) Функция является симметричной относительно прямой х = а, т.к. разность

(х – а) входит в функцию плотности распределения в квадрате.

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.

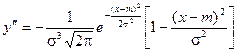
При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно .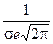

Построим график функции плотности распределения.

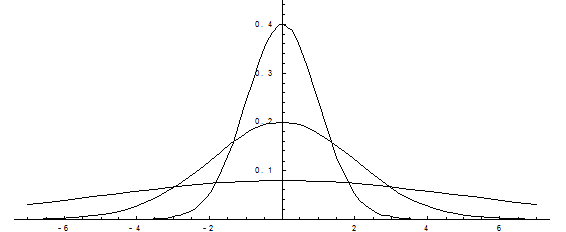
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой: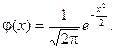

Для краткости говорят, что СВ Х подчиняется закону N(m, s), т.е. Х ~ N(m, s). Параметры m и s совпадают с основными характеристиками распределения: m = m_X, s = s_Х = 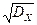. Если СВ Х ~ N(0, 1), то она называется стандартизованной нормальной величиной. ФР стандартизованной нормальной величиной называется функцией Лапласа и обозначается как Ф(x). С ее помощью можно вычислять интервальные вероятности для нормального распределения N(m, s):

P(x₁ £ X < x₂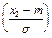) = Ф - Ф .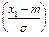

При решении задач на нормальное распределение часто требуется использовать табличные значения функции Лапласа. Поскольку для функции Лапласа справедливо соотношение Ф(-х) = 1 - Ф(х), то достаточно иметь табличные значения функции Ф(х) только для положительных значений аргумента.

Для вероятности попадания на симметричный относительно математического ожидания интервал справедлива формула: P( |X - m_X| < e ) = 2×Ф(e/s) - 1.

Центральные моменты нормального распределения удовлетворяют рекуррентному соотношению: m_n+2 = (n+1)s²m_n, n = 1, 2, ... . Отсюда следует, что все центральные моменты нечетного порядка равны нулю (так как m₁ = 0).

Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

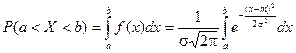
Обозначим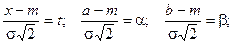

Тогда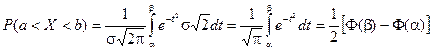

Т.к. интеграл 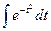не выражается через элементарные функции, то вводится в рассмотрение функция

,

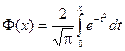которая называется функцией Лапласаили интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

Ниже показан график функции Лапласа.

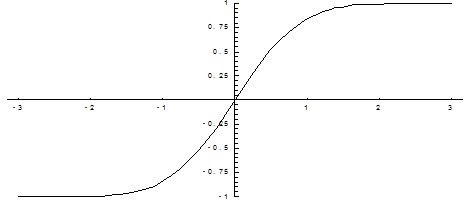
Функция Лапласа обладает следующими свойствами:

1) Ф(0) = 0;

2) Ф(-х) = - Ф(х);

3) Ф(¥) = 1.

Функцию Лапласа также называют функцией ошибок и обозначают erf x.

Еще используется нормированнаяфункция Лапласа, которая связана с функцией Лапласа соотношением:

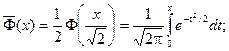
Ниже показан график нормированной функции Лапласа.

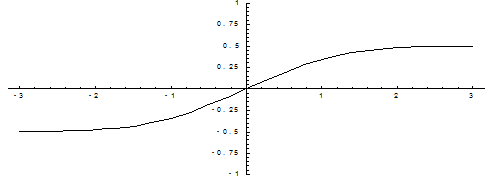
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

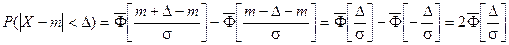
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

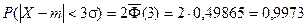
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.

Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.

Получаем:

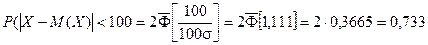
Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Плотность распределения имеет вид:

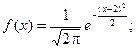
Построим график:

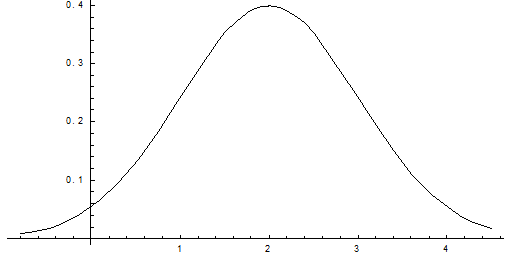
Найдем вероятность попадания случайной величины в интервал (1; 3).

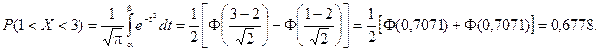
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.

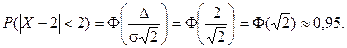
Тот же результат может быть получен с использованием нормированной функции Лапласа.

Лекция 8 Закон больших чисел(Раздел 2)

План лекции

Центральная предельная теорема ( общая формулировка и частная формулировка для независимых одинаково распределенных случайных величин).

Неравенство Чебышева.

Закон больших чисел в форме Чебышева.

Понятие частоты события.

Статистическое понимание вероятности.

Закон больших чисел в форме Бернулли.

Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачивает случайный характер и становится закономерным (иначе говоря, случайные отклонения от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем, называемой законом больших чисел.

ЗАКОН БОЛЬШИХ ЧИСЕЛ – общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Первым примером действия этого принципа может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (часто использующееся на практике, например, при использовании частоты встречаемости какого-либо качества респондента в выборке как выборочной оценки соответствующей вероятности).

Сущность закона больших чисел состоит в том , что при большом числе независимых опытов частота появления какого-то события близка к его вероятности.

Центральная предельная теорема (ЦПТ) ( в формулировке Ляпунова А.М. для одинаково распределенных СВ). Если попарно независимые СВ X₁, X₂, ..., X_n, ... имеют одинаковый закон распределения с конечными числовыми характеристиками M[X_i] = m и D[X_i] = s², то при n ® ¥ закон распределения СВ 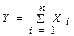неограниченно приближается к нормальному закону N(n×m, ).

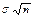Следствие. Если в условии теоремы СВ 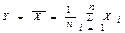, то при n ® ¥ закон распределения СВ Y неограниченно приближается к нормальному закону N(m, s/ ).

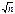Теорема Муавра-Лапласа.Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n ® ¥ и фиксированном значении вероятности “успеха” в одном испытании p закон распределения СВ K неограниченно приближается к нормальному закону N(n×p, ).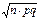

Следствие. Если в условии теоремы вместо СВ К рассмотреть СВ К/n - частоту “успехов” в n испытаниях по схеме Бернулли, то ее закон распределения при n ® ¥ и фиксированном значении p неограниченно приближается к нормальному закону N(p, ).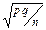

Замечание. Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Законом распределения такой СВ является биноминальный закон. Тогда при n ® ¥ биноминальный закон имеет два предельных распределения:

n распределение Пуассона (при n ® ¥ и l = n×p = const);

n распределение Гаусса N(n×p, 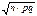) (при n ® ¥ и p = const).

Пример. Вероятность “успеха” в одном испытании всего лишь p = 0,8. Сколько нужно провести испытаний, чтобы с вероятностью не менее 0,9 можно ожидать, что наблюдаемая частота “успеха” в испытаниях по схеме Бернулли отклонится от вероятности p не более чем на e = 0,01?

Решение. Для сравнения решим задачу двумя способами:

а) На основе второго неравенства Чебышева имеем:

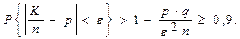
Следовательно: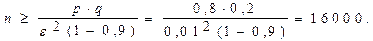

б) Используя теорему Муавра-Лапласа и учитывая, что если СВ Y ~N(m, s), то 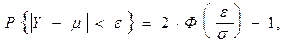получаем:

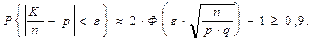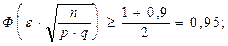
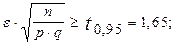
Следовательно: 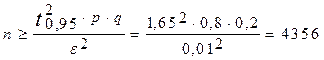, т.е. почти в четыре раза меньше.

При этом полученное значение настолько велико, что погрешностью используемой формулы можно пренебречь.

Задача 2. По полосе укреплений противника осуществляется залп из 100 орудий. При стрельбе из одного такого орудия математическое ожидание числа попаданий равно 2, а среднеквадратическое отклонение числа попаданий равно 1,5. Найти приближенно вероятность того, что в полосу укреплений противника попадет от 180 до 220 снарядов.

Задача 3. Противник атакует полосу укреплений, используя в наступлении 50 танков. Вероятность вывода из строя танка в этом бою равна 0,4. Если выведено из строя не менее 35% танков, то противник прекращает свое наступление. Требуется найти вероятность того, что противник откажется от наступления.

Следующие утверждения и теоремы составляют основу законов, объединенных общим названием закон больших чисел.

Первое неравенство Чебышева. Если СВ X ³ 0 имеет конечное значение m = M[X], то для любого e > 0 справедливо:

P{X ³ e} £ m/e или P{X < e} > 1 - m/e.

Второе (основное) неравенство Чебышева. Если СВ X имеет конечные значения m = M[X] и s² = D[X], то для любого e > 0 справедливо:

P{ôX - mô ³ e} £ s²/e² или P{ôX - mô < e} > 1 - s²/e².

Последовательность СВ X₁, X₂, ..., X_n, ... называется сходящийся по вероятности при n ® ¥ к СВ X (обозначение: 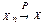при n ® ¥), если для любого, сколь угодно малого e > 0 справедливо 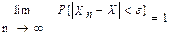, или, иными словами, для любых, сколь угодно малых чисел e > 0 и d > 0 найдется номер k, что для всех n > k выполняется условие:

P{ôX_n - Xô < e} > 1 - d.

Теорема (Закон больших чисел в форме Чебышева). Если попарно независимые СВ X₁, X₂, ..., X_n, ... имеют конечные значения M[X_i] = m_i и D[X_i] = s_i²£ s², то для любого e > 0 справедливо следующее:

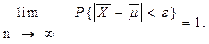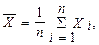
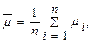где или 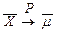при n ® ¥.

Следствие. Если в условии теоремы СВ X₁, ..., X_n, ... имеют одинаковые значения M[X_i] = m, то для любого e > 0 справедливо следующее:

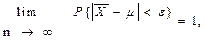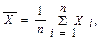где или 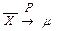при n ® ¥.

Теорема (Закон больших чисел в форме Бернулли). Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n ® ¥ частота “успехов” сходится по вероятности к p, где p - вероятность “успеха” в одном испытании, т.е.:

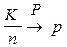при n ® ¥ или 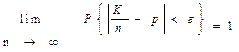для любого e