Нормальный закон распределения
Нормальный закон распределения (закон Гаусса) характеризуется плотностью
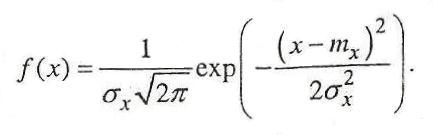
В экономике часто встречаются случайные величины, распределение по нормальному закону.
Нормальный закон распределения возникает там, где случайная величина образуется в результате совокупного влияния многих других случайных факторов.
Нормальное распределение характеризуется тем, что крайние значения случайной величины в нем встречаются достаточно редко, а значения, близкие к средней величине - достаточно часто (рис. 2.3).
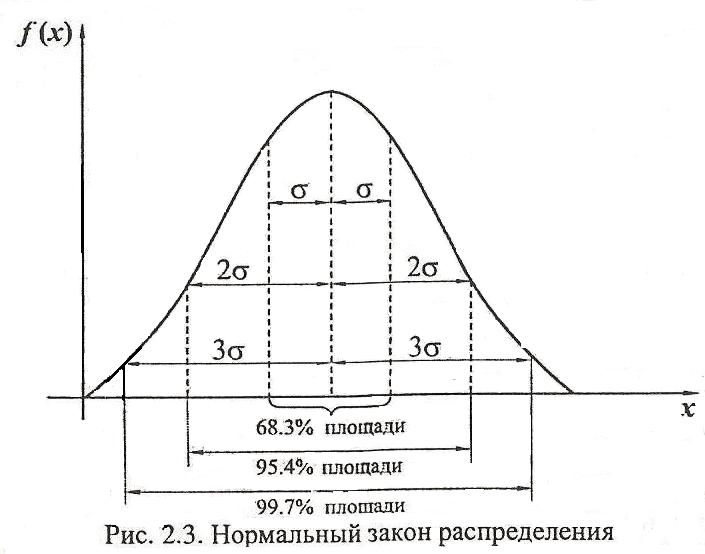
Нормальный закон - это двухпараметрический закон. Параметр mx определяет положение центра рассеяния случайной величины, а параметр σх характеризует меру ее рассеяния относительно центра
Функция распределения нормального закона не выражается в явном виде через элементарные функции. Она может быть представлена следующим образом:
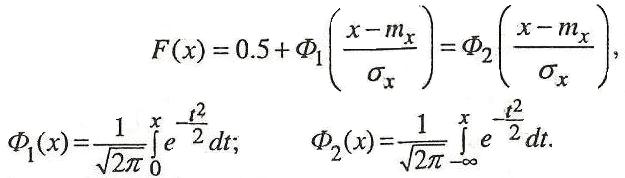
Здесь Ф1(х), Ф2(х)- функции Лапласа (интегралы вероятностей). Эти функции табулированы и широко используются в практических расчетах.
Возьмем за основу функцию Ф1(х), будем обозначать ее Ф(х) (без индекса), и именно ее будем иметь в виду, говоря о функции Лапласа.
Функция Лапласа Ф(х)имеет следующие свойства:
Ф(-∞) = -0,5, Ф(+∞) = +0,5, Ф(-х) = - Ф(х), Ф(0) = 0
Для центральных моментов существует рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков:
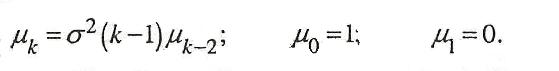
Вероятность попадания нормальной случайной величины Х на участок от α до β выражается через функцию Лапласа следующим образом:
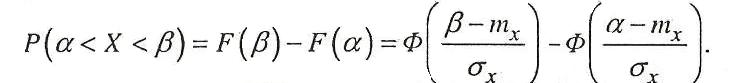
Найдем вероятности попадания нормальной случайной величины в отрезки, длина которых равна σ.

Правило трех сигм для нормального закона можно выразить соотношением:
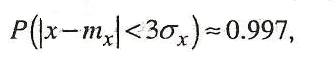
то есть с точностью до тысячных весь диапазон разброса значений случайной величины с нормальным законом распределения заключен в пределах ±3σх от центра величины.
Если исследователю известно, что изучаемый экономический показатель подчиняется нормальному закону распределения, то знание математического ожидания и среднего квадратического отклонения (дисперсии) дает ему основание осуществить прогноз развития экономической ситуации.
Если случайная величина подчиняется нормальному закону, то с вероятностью 0.683 результат любого единичного ее измерения лежит в интервале тх ± σх; с вероятностью 0.954 он попадает в интервал тх± 2σх; с вероятностью 0.997 - в интервал тх ± 3σх.
Например, пусть известно, что среднее значение доходности акций фирмы равно 15% при среднеквадратичном отклонении σх=3%. Тогда, если доходность, акций подчиняется нормальному закону распределения, прогнозируемая доходность по акциям фирмы будет лежать в диапазоне 15±6% с вероятностью 0.954 и в диапазоне 15±9% вероятностью 0.997.
Дата добавления: 2016-06-15; просмотров: 5132;











