Корневые подпространства.

Ядро линейного преобразования 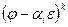назовем корневым подпространством высоты k и обозначим через 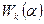. Корневое подпространство 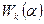отлично от нулевого вектора, только если 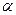является корнем характеристического многочлена. Линейное пространство над полем комплексных чисел расщепляется в прямую сумму корневых подпространств (Следствие 1.6). В дальнейшем, рассмотрим возможность дальнейшего расщепления корневых подпространств в прямую сумму инвариантных подпространств. Будем говорить, что вектор 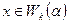имеет высоту k, если 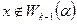. Приведем ряд свойств корневых подпространств.

Свойство 1.4.

Доказательство очевидно.

Свойство 1.5. Если , то .

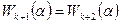Доказательство. Если 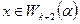, то 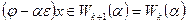, и, значит 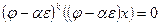, что равносильно включению 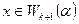. Тем самым установлено включение 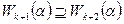, объединив которое с обратным включением (Свойство 1.4) выводим требуемое утверждение.

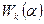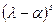Минимальный аннулирующий многочлен корневого пространства является делителем многочлена , и, значит, равен , где 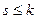. Из определения корневого подпространства вытекает равенство .

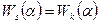Свойство 1.6. Если размерность корневого подпространства равна степени минимального многочлена этого подпространства, то корневое подпространство не представимо в виде прямой суммы инвариантных подпространств меньших размерностей.

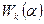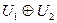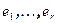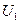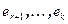Доказательство. Пусть k – степень минимального многочлена корневого подпространства и корневое подпространство представляется в виде прямой суммы инвариантных подпространств меньших размерностей. Пусть - базис , а базис 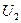. Система векторов 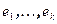является базисом 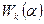и, значит, минимальный аннулирующий многочлен пространства равен наименьшему общему кратному минимальных аннулирующих многочленов этих векторов. Следовательно, среди векторов 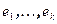найдется такой вектор, минимальный аннулирующий многочлен которого равен . Не нарушая общности можно считать, что это вектор 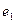. Система векторов 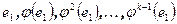линейно независима и принадлежит 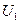в силу инвариантности подпространства. Поскольку в построенной системе k векторов, то размерность 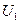не меньше k, что противоречит допущению.