Точность РАС при произвольных воздействиях .Коэффициенты ошибок.

Считаем, что x(t) = 0, а λ(t) существует только при t ≥ 0 и изменяется медленно. Представим ПФ замкнутой системы по ошибке в виде

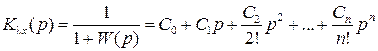. (5.10)

Коэффициенты полученного ряда C_j называются коэффициентами ошибок. Смысл первых коэффициентов ошибок уже известен из результатов п. 5.1 : C₀ = X_пол , C₁ = X_ск , C₂ = X_уск .

Это позволяет определить динамическую ошибку РАС:

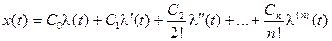. (5.11)

Таким образом, чтобы найти ошибку в установившемся режиме (t → ∞ или p → 0) при произвольных воздействиях и системах, необходимо:

‒ определить ПФ замкнутой системы по ошибке (5.4) и представить её в виде отношения двух полиномов:

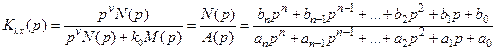, (5.12)

‒ вычислить коэффициенты ошибок C_j;

‒ вычислить производные входного воздействия (t → ∞) : λ′(t), λ″(t), …, λ⁽ⁿ⁾(t);

‒ найти динамическую ошибку по формуле (5.11) и записать установившееся значение ошибки в виде

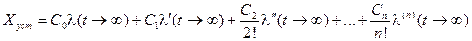. (5.13)

Существует несколько способов вычисления коэффициентов ошибок: разложение (5.12) в ряд с учетом того, что p → 0 :

;

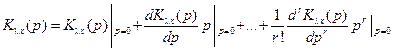деление полинома числителя на полином знаменателя и т. д.

Мы рассмотрим только наиболее простые способы, удобные для вычислений в инженерной практике.

Первый способ. Приравняем (5.10) и (5.12), что в результате дает

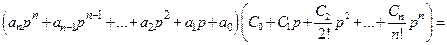
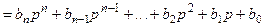. (5.14)

Приравнивая коэффициенты при одинаковых степенях pⁿ, получаем формулы для последовательного вычисления коэффициентов ошибок:

, , , ,

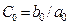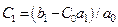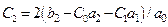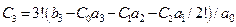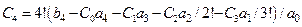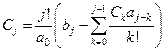, . (5.15)

Второй способ[1, 4]. От (5.14) можно перейти к полиномам M(p) и N(p) ПФ разомкнутой системы (5.3) с порядком астатизма v. Пусть полином числителя M(p) имеет вид .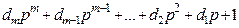

После подстановки этих условий в (5.14) получим

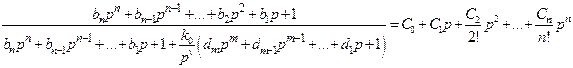. (5.16)

После переноса знаменателя левой части в правую и приведения подобных можно найти связь коэффициентов C_j с коэффициентами полиномов M(p) и N(p), приравнивая коэффициенты при одинаковых степенях pⁿ [1, 4] .

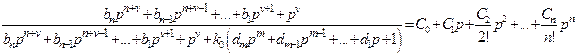. (5.17)

Операции по (5.17) существенно сложнее, чем по (5.14), но позволяют проводить вычисления по ПФ разомкнутой системы. Приведем несколько готовых результатов из [4] при различных порядках астатизма v.

v = 0. , , .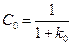

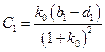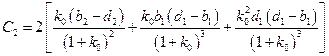v = 1. , , .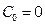

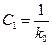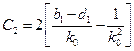v = 2. 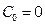, , 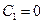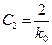. (5.18)

Анализ подтверждает результаты, полученные в п. 5.1: для астатической системы порядка v первые v коэффициентов ошибок равны нулю (C_v-1 = 0, C_v-2 = 0,…, C₀ = 0), и лишь начиная с C_v, получаются ненулевые коэффициенты.

Пример 5.1. Определим динамическую ошибку РАС ФАПЧ из примера 4.2 при входном воздействии λ(t) = (λ₀ + λ₁t + λ₂t²)1(t) при отсутствии возмущения ξ(t).

Запишем ПФ разомкнутой системы (4.9) в виде

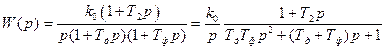. (5.19)

Воспользуемся вторым способом: v = 1, d₁ = Т₂, d₀ = 1, b₂ = Т_дТ_ф, b₁ = Т_д + Т_ф, b₀ = 1.

Подставляя эти коэффициенты в (5.18), получаем

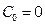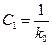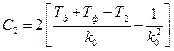, , . (5.20)

Теперь необходимо найти первые две производные λ(t):

λ′(t) = (λ₁ + 2λ₂t), λ″(t) = 2λ₂. (5.21)

В результате из (5.11) получаем

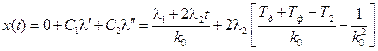, (5.22)

а .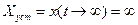

Таким образом, для получения конечной ошибки в установившемся режиме в систему необходимо добавить еще один идеальный интегратор. Увеличение k₀ и Т₂ уменьшает значение ошибки, а повышение Т_д, Т_ф – увеличивает ошибку.

Рассмотрим вычисление коэффициентов C_j первым способом.

Для этого необходимо получить ПФ по ошибке:

K_λx(p) = 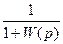= 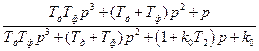. (5.23)

b₃ = Т_дТ_ф, b₂ = Т_д + Т_ф, b₁ = 1, b₀ = 0, а₃ = Т_дТ_ф,

а₂ = Т_д + Т_ф, а₁ = 1 + k₀Т₂, а₀ = k₀.

После вычислений по формулам (5.15) получим те же результаты, что и первым способом в (5.20). Искать C₃ смысла нет, так как производные λ(t), начиная с третьей, равны нулю.

В данном примере второй способ оказался эффективнее.

5.3. Ошибка в установившемся режиме
при гармоническом воздействии

В задачах анализа и синтеза РАС широко используются частотные методы. В этом случае оказывается полезной оценка установившейся ошибки при гармоническом воздействии.

При гармоническом воздействии использовать метод коэффициентов ошибок затруднительно, поскольку число производных гармонических функций не ограничено. Для оценки ошибок в этом случае удобно использовать частотные характеристики.

Пусть входное воздействие 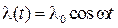. Тогда установившаяся ошибка также будет гармоническим колебанием с той же частотой.

Определим АЧХ и ФЧХ ошибки .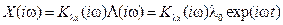

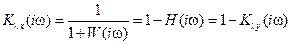. (5.24)

Найдем модуль и аргумент ПФ по ошибке:

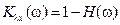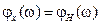, . (5.25)

Имея АЧХ и ФЧХ замкнутой системы, можно определить АЧХ и ФЧХ ошибки системы.

Рассмотрим ряд случаев.

1. Пусть система статическая (рис. 5.2):

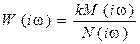, тогда

.

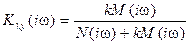На нулевой частоте в этом случае получается:

, .

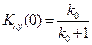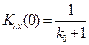2. Для астатической системы (рис. 5.3):

, ;

, .

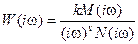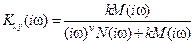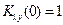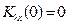Ошибка РАС будет максимальной при максимальной амплитуде входного воздействии: .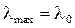

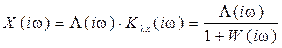, откуда .

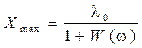Для того, чтобы уменьшить ошибку
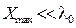( ), необходимо, чтобы W(ω) >> 1, что у астатической системы выполняется только в области нижних частот (ОНЧ – до частоты первого сопряжения на ЛАЧХ).

Если на заданной частоте ω₀, лежащей в ОНЧ, заданы Х_max и величина воздействия λ₀, то должно выполниться условие (рис. 5.4) 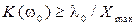или

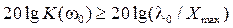. (5.26)

При проектировании РАС из заданных условий точности на определенных частотах задаются контрольные точки, которые наносятся на ЛАЧХ. График ЛАЧХ проектируемой РАС должен проходить не ниже контрольных точек (рис. 5.4).