Точность системы в установившемся режиме при полиномиальном

Воздействии.

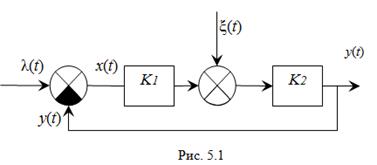
Рассмотрим обобщенную схему РАС, представленную на рис. 5.1.

С помощью формул гл. 2 запишем ПФ замкнутой системы по воздействию:

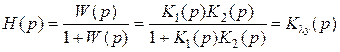, (5.1)

по ошибке :

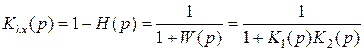. (5.2)

Представим ПФ разомкнутой системы в виде

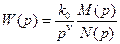, (5.3)

где v – число идеальных интеграторов (порядок астатизма РАС), k₀ – коэффициент усиления разомкнутой системы по постоянному напряжению, M(p) и N(p) – полиномы, свободные члены которых равны единице, степень полинома числителя у реальных РАС не превышает степень полинома знаменателя.

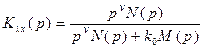, (5.4)

В стационарном режиме (при t → ∞ или p → 0)

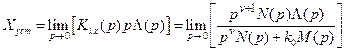. (5.5)

Рассмотрим несколько важных случаев (x(t) = 0).

1. Пусть система W(p) статическая (v = 0). Найдем ошибку при воздействии статическом 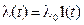и с постоянной скоростью 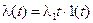. Для этого проанализируем составляющие ошибки при воздействии 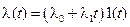, изображение по Лапласу которого .

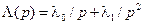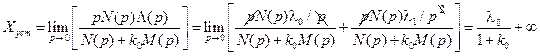. (5.6)

Таким образом, при статическом воздействии на статическую РАС получается конечная ошибка, называемая ошибкой по положению: .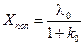

Однако при воздействии с постоянной скоростью установившаяся ошибка статической РАС стремится в бесконечность.

2. Введем в систему один идеальный интегратор, тогда система W(p) будет астатическойпервого порядка (v = 1). Проанализируем составляющие ошибки при воздействии 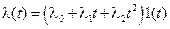, изображение по Лапласу которого .

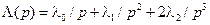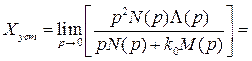
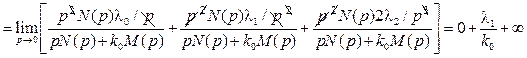. (5.7)

Таким образом, при статическом воздействии на астатическую РАС первого порядка установившаяся ошибка стремится к нулю.

При воздействии с постоянной скоростью на ту же РАС получается конечная установившаяся ошибка, называемая ошибкой по скорости: .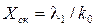

Однако при воздействии с постоянным ускорением установившаяся ошибка астатической РАС первого порядка стремится в бесконечность.

3. Введем в систему еще один идеальный интегратор, тогда система W(p) будет астатическойвторого порядка (v = 2). Проанализируем составляющие ошибки при том же воздействии .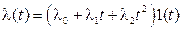

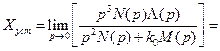
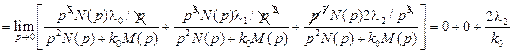. (5.8)

Ошибки по положению и по скорости астатической РАС второго порядка равны нулю. Останется только ошибка по ускорению

.

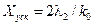Проведенный анализ позволяет сделать такие выводы.

При полиномиальном воздействии порядка n( 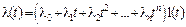, 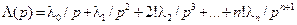) на астатическую РАС порядка v:

при n < v установившаяся ошибка стремится к нулю;

при n > v установившаяся ошибка стремится в бесконечность;

при n = v ошибка в установившемся режиме определяется формулой

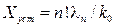. (5.9)

Чем больше k₀, тем меньше ошибка в установившемся режиме.

Но следует помнить о том, что увеличение k₀ снижает запас устойчивости РАС.