Численные решения СЛАУ.

Метод Гаусса.

Пусть задана система линейных уравнений Ax=U с плотной матрицей, элементы которой хранятся в оперативной памяти.

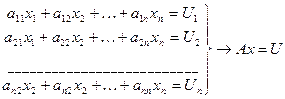
Переходим к системе (исключения х₁)

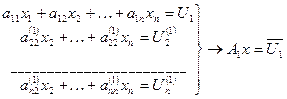
Эта операция равносильна умножению Ax=U слева на матрицу

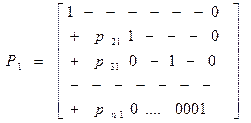
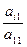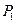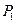где p_i1= i=2,3…n A₁ x= U₁à Ax= U

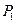a_ij⁽¹⁾= a_ij- a_ij

Следующий переход к системе (исключения х₂)

Это исключения равносильно умножению A₁ x= U ₁ слева на матрицу Р₂:

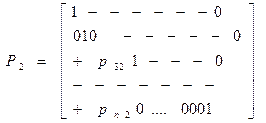
где p_i2= 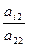i=3,4…n a_ij⁽²⁾= a_ij⁽¹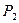⁾ - a_2j⁽¹⁾

A₁ x= U₁=> 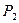A₁х = 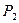U₁àP₂P₁Ax= P₂P₁ U

Продолжая этот процесс и так далее, мы придем к легко решаемой системе уравнений с треугольной матрицей A_n-1х =U_n-1

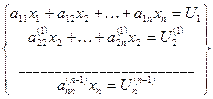
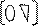A_n-1 =

A_n-1- верхняя треугольная матрица. Здесь A_n-1х=U_n-1=> =P_n-1P_n-2Ax= P_n-1P_n-2 U, так что A =(P_n-1P_n-2 …P₁)^-1 A_n-1х

P Q

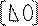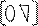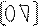
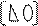A = *

Где матрица P- нижняя треугольная, а Q- верхняя треугольная. Решение по методу Гаусса сводится к разложению A на произведение двух треугольных матриц. Одна из них

P~ с единицами по главной диагонали и на верхнюю треугольную

Q~

Заметим, что

det A=det P*det Q= a₁₁ a₂₂⁽¹⁾ a₃₃⁽²⁾… a_nn^(n-1)

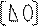Если представления матрицы A в виде PQ найдены, то решение системы Ax=U сводится к решению двух треугольных систем уравнений.

Py= U ↓ (y)

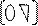Ax=U=>PQx=U=>

Qx= y ↑ (x)

Решения по методу Гаусса сводится фактически к решению системы Py= U ↓

При прямом ходе, а затем к решению системы Qx= y ↑ при обратном ходе.

Разложение матрицы на две треугольные матрицы называется процессом факторизации (триангуляция) матрицы, т.е. представление матрицы в виде A=PQ.

После вычисления прямого хода мы получаем матрицу A_n-1= Q

Метод Холецкого, прогонки приводят к факторизации матрицы A.

Метод Холецкого.

Пусть дана невырожденная матрица размером N*N (det A≠0) Представим её в виде произведения

A=BC (1) A~(a_ij) B~(b_ij) C~(c_ij)

k>i

b_ik=0, когда k>i

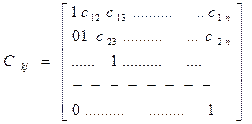
c_kj=0 при k>j c_jj =1

Из (1) следует

a_ij= b_ik c_ki

Преобразуем эту сумму двумя способами

a_ij= b_ik c_ki= b_ik c_ki+ b_ii c_ij+ b_ik c_ki= 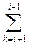b_ik c_ki+ b_ii c_ij

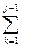a_ij= b_ik c_kj= b_ik c_kj+ b_ij c_jj+ 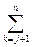b_ik c_kj= 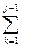b_ik c_kj+ b_ij c_jjà b_ij c_jj= a_ij- 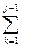b_ik c_kj

Отсюда находим

b_ij= 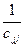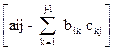i ≥ j b₁₁=a₁₁ c_jj=1

c_jj= 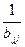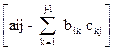при I < j

Матрицы B и C найдены, тогда Ax= BCx=U

By=U ↓ (y) прямой ход

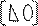
Cx=y ↑ (x) обратный ход

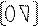
Лекция 8

Метод прогонки.

Решение многих задач для обыкновенных дифференциальных уравнений и уравнений в частных производных приводит к системам линейных уравнений с матрицами специального вида, для решения которых целесообразно применять не общие методы, а методы, использующие специфику полученной системы.

Пусть требуется найти решение следующей системы трехточенных уравнений.

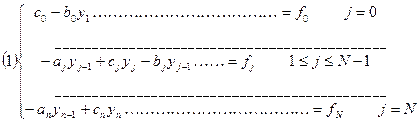
Или в векторной форме

A 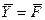(2)

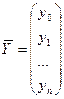
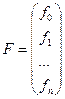
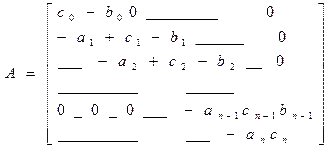
A=

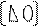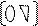По методу Гаусса A= * = *

Факторизация ленточных матриц, т.е. разложение их на произведение двух треугольных матриц A=PQ

(нижней и верхней) треугольных матриц может быть произведено так, что P и Q также будут ленточными матрицами.

Перейдем к следующей системе (3)

y_j=p_j+1y_j+1+q_j+1 (3)

Где p_j+1 и q_j+1 неизвестные числа

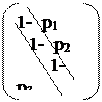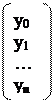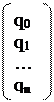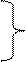u₀- p₁u₁ =q₁

u₁- p₂u₂ =q₂ =

u₀- p₁u₁ =q₃

Числа p_j и q_j можно искать из системы (1), т.к.

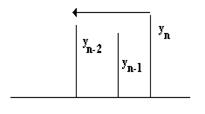
y_j-1=p_jy_j+q_j (4)

Подставляя (4) в систему (1) получим

-a_j(p_j y_j+ q_j)+c_j y_j-b_j y_j+1=f_j

(c_j-a_j p_j)y_j=b_j y_j+1 +(f_j+ a_j q_j)

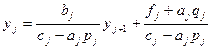(5)

Сравнивая (5) с(3) получим

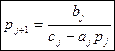
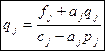(6)

Из 1^го крайнего условия

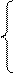
y₀ =p₁y₁+q₁

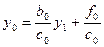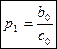
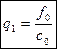=> (7)

Из 2^го крайнего условия

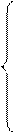y_n-1= p_ny_n+q_n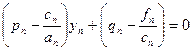

-a_n y_n-1+c_ny_n=f_{n 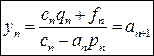(8)}

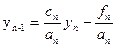
Теперь с помощью (3) получим

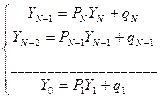
Проверка метода прогонки на устойчивость.

Поскольку вычисления p_j и q_j производятся по рекуррентным формулам, то в зависимости от элементов матрицы A: a_i, b_i, c_i, то неизбежны ошибки округления при вычислении по рекуррентным формулам p_j и q_j. Эти ошибки могут быстро возрастать и сделать вычисления непригодными. Поведение ошибки dp_j+1 можно проследить, положив её приближённо равной дифференциалу функции.

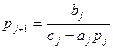
Имеем

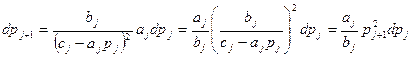(9)

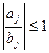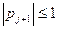Прогонка будет устойчивой, если и (10)

Тогда dp_j+1 <dp_j

Эти неравенства (10) будут выполнены, если, например, положить, что коэффициент матрицы A удовлетворяют следующие условия

0≤ a_j≤b_j

c_j≥ a_j+b_j (11) j=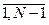

0<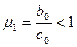

В самом деле

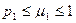, отсюда

<

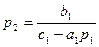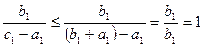
Вообще, проверяется p_j+1≤ 1 для j=1,n-1

При этих условиях при вычислении p_j+1 накопление ошибки не происходит. Аналогично из равенств

;

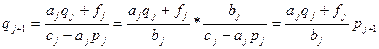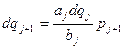<dq_j

Т.к. при тех же условиях (11) нарастания погрешностей при вычислении q _j+1 не происходит.

Лекция 9