Метод ньютона (касательных).

Если уравнение 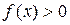имеет корень 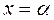и непрерывную производную 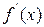на отрезке 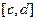, то функцию 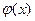можно выбрать в виде

.

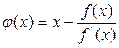В результате задача определения корня 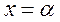уравнения 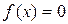сводится к отысканию корня уравнения

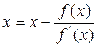. (1)

Итерационный метод решения уравнения, использующий преобразование исходного уравнения к виду (1), называют методом Ньютона. При этом получим следующую рекуррентную формулу

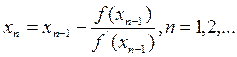(2)

Построим график функции 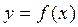. Уравнение касательной в точке 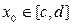будет иметь вид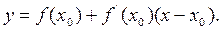

Найдём точку 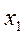пересечения этой касательной с осью у. Так как при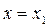 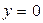, то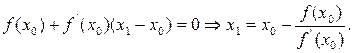

Тот же результат получим из соотношения (2) при 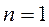. Следовательно, первое приближение 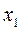корня можно найти и геометрически с помощью касательной к графику функции 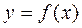в точке 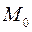. Аналогичным путём можно построить второе 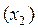и последующие приближение. Отсюда название метод касательных.

Следует отметить, что при 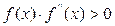сходимость алгоритма метода Ньютона будет наблюдаться при любых начальных приближениях в интервалах .

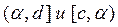При 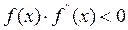сходимость итерационного процесса будет обеспечиваться при выборе начального приближения из условия

,

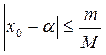где m, M – некоторые положительные константы, для которых

,

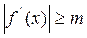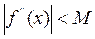
для всех .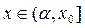

Приведём алгоритм решения уравнения методом Ньютона в виде блок – схемы:

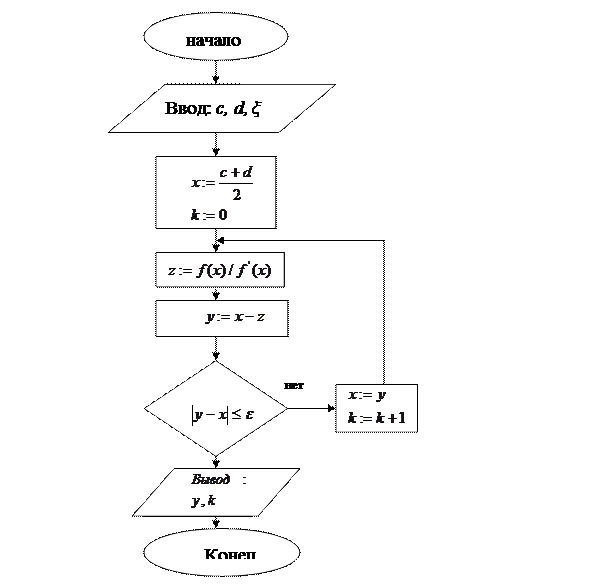
Метод Ньютона обеспечивает более быструю сходимость, чем метод простой итерации.

В заключение следует отметить, что при решении нелинейных уравнений