Погрешность арифметической операции

Арифметические действия над приближенными числами приводят к накоплению погрешности результата решения математической задачи. Пусть α, в, α_n и в_n – некоторые числа и их приближенные значения, α◦в- некоторая арифметическая операция над числами. Тогда абсолютную и относительную погрешности арифметических операций будем записывать в виде

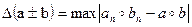
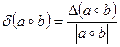
При этом если ∆α >0 и ∆b>0, то

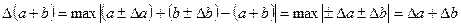
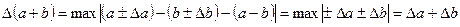
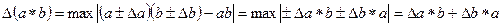
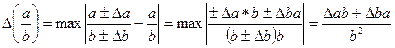
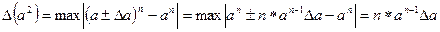
Используя данные результаты можно оценить и относительные погрешности

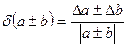
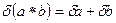
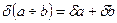
δ(αⁿ)=nδα

При оценке погрешности вычисления функций y=f(x) для придельных значений абсолютных и относительных погрешностей используем равенства

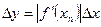
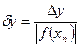
где x_n- приближённое значение величин х, ∆x- придельная погрешность.

Алгоритмы являются строгим описанием последовательности операций. Общие свойства алгоритмов:

1) Массовость- применимость ко всем задачам рассматриваемого класса при любых исходных данных или с оговариваемыми границами их изменения.

2) Определенность- любой шаг алгоритма не должен допускать толкования.

3) Дискретность- представимость всякого процесса в виде последовательности выполняемых друг за другом отдельных законченных шагов.

4) Результативность- получение результата за конечное число действий, причем с требуемой точностью.

Лекция 2