Интерполяционный многочлен Лагранжа

Интерполяционная формула Лагранжа используется для произвольно заданных узлов интерполирования.

Пусть в точках x₀, x₁, …, x_n таких, что a£ x₀<…< x_n£b, известны значения функции y=f(x), т.е. на отрезке [a, b] задана табличная (сеточная) функция

Требуется построить некоторую функцию P_n(x) степени не выше n, имеющую в заданных узлах x₀, x₁, …, x_n те же значения, что и функция f(x). С этой целью представим P_n(x) в следующем виде:

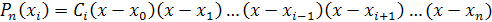
где С_i – некоторая константа, которая определяется из следующего уравнения:

.

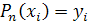В этом случае для многочлена:

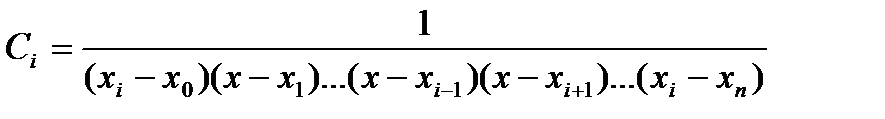
Подставляя выражение для константы С_i в исходную зависимость полинома для каждого i=0,1,2,…, n следующее значение многочлена:

,

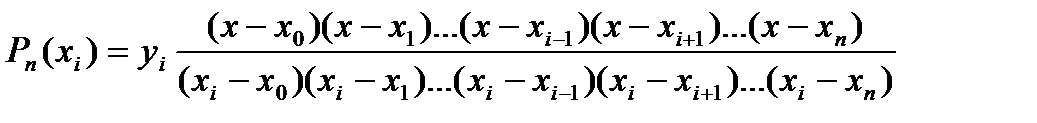Подставляя значение P_n(x) для всех точек от 0 до n, получим следующее выражение для многочлена Лагранжа:

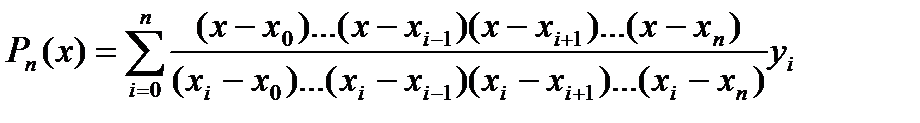
Пример 4.1.1. Построить интерполяционный полином для функции y=sin x.

Возьмем сетку, состоящую из трех точек: x₀=0; x₁= 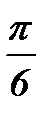; x₂= 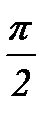, выпишем соответствующие этим аргументам значения функции sin x: y₀=0; y₁= 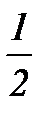; y₂=1.

Построим по этой таблице интерполяционный полином второй степени, использую формулу Лагранжа:

.

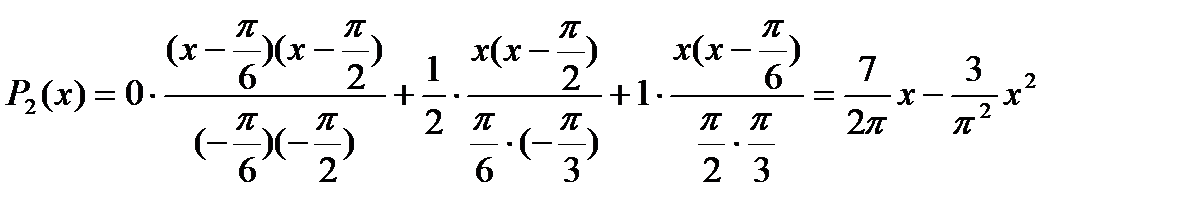Проверяем, что в точках сетки этот полином принимает нужные значения. Оценим погрешность интерполирования, сравнив значения sin x и интерполяционного полинома в точке х= .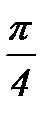

.

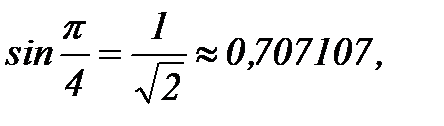
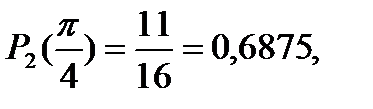
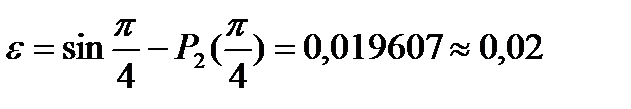Значительная величина погрешности определяется тем, что на отрезке длиной 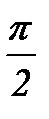мы взяли грубую сетку, состоящую всего из трех точек. Чтобы улучшить точность интерполирования, нужно либо увеличить число точек n и повысить соответственно степень интерполяционного полинома P_n(x), либо уменьшить длину исходного отрезка.