Интерполяционный многочлен Ньютона

<3 4 567 8 9 >

Предположим дополнительно, что рассматриваемые значения аргумента являются равноотстоящими, т. е. образуют арифметическую прогрессию.

В этом случае шаг таблицы h = х_i+1 - x_i (i = 0, 1, 2, ..., n) = const является величиной постоянной. Для таких таблиц построение интерполяционных формул (как впрочем, и вычисление по этим формулам) заметно упрощается.

Прежде чем перейти к рассмотрению этого вопроса, познакомимся с понятием конечных разностей.

Пусть функция задана таблицей с постоянным шагом. Разности между значениями функции в соседних узлах интерполяции называют конечными разностями первого порядка:

Δ y_i = y_i+1 - y_i (i = 0, 1, 2, ...).

Из конечных разностей первого порядка образуются конечные разности второго порядка:

Δ ²y_i = Δ yⁱ⁺¹- Δ y_i (i = 0, 1, 2, ...)

Для записи конечных разностей используются горизонтальные и диагональные таблицы.

Горизонтальная таблица

x	y	Δy	Δ²y	Δ³y
x₀	y₀	Δy₀	Δ² y₀	Δ³y₀
x₁	y₁	Δy₁	Δ² y₁
x₂	y₂	Δy₂
x₃	y₃

Диагональная таблица

x	y	Δy	Δ²y	Δ³y
x₀	y₀	Δy₀	Δ² y₀	Δ³y₀
x₁	y₁
Δy₁
x₂	y₂	Δ² y₁
Δy₂
x₃	y₃

Формула Ньютона «вперед»:

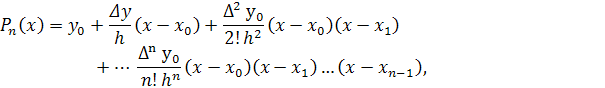
где n – порядок полинома, h – шаг (расстояние между узлами).

Первый порядок:

x₁=x₀-h	Δy= y₁ – y₀
x₂=x₀-2h	Δy₁= y₂ – y₁
x_n=x₀-n×h	Δy_n-1= y_n – y_n-1

Второй порядок:

Δ²y= Δy₁ – Δy₀

Δ²y₁= Δy₂ – Δy₁

Δ²y_n-₂= Δy_n_-1 – Δy_n-₂

Формула Ньютона «назад»:

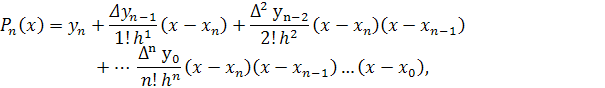
Программа для интерполирования «вперед»:

Программа для интерполирования «назад»:

program newton; const n=3; var d:array[0..n,0..n] of real; x,y:array[0..n] of real; p:array[1..n] of real; f1,f2:text; h,x1,s1:real;i,j:integer; begin assign(f1,'n1.pas');assign(f2,'nnn.pas'); reset(f1);rewrite(f2);x1:=1.5;h:=1; for i:=0 to n do read(f1,x[i],y[i]); s1:=y[0]; for i:=0 to n do d[i,0]:=y[i]; for j:=1 to n do for i:=0 to n-j do d[i,j]:=d[i+1,j-1]-d[i,j-1]; for i:=1 to n do begin p[i]:=1;for j:=1 to i do p[i]:=p[i]*(x1-x[j-1])/(h*j); s1:=s1+d[0,i]*p[i]; end; write(f2,s1:7:4);close(f2);end.

program newton; const n=3; var d:array[0..n,0..n] of real; x,y:array[0..n] of real; p:array[1..n] of real; f1,f2:text; h,x1,s1:real;i,j:integer; begin assign(f1,'n1.pas');assign(f2,'nn3.pas'); reset(f1);rewrite(f2);x1:=1.5;h:=1; for i:=0 to n do read(f1,x[i],y[i]);s1:=y[n]; for i:=0 to n do d[i,0]:=y[i]; for j:=1 to n do for i:=0 to n-j do d[i,j]:=d[i+1,j-1]-d[i,j-1]; for i:=1 to n do begin p[i]:=1;for j:=1 to i do p[i]:=p[i]*(x1-x[n-j+1])/(h*j); s1:=s1+d[n-i,i]*p[i]; end; write(f2,s1:5:2);close(f2);end.

4.2. Итерационные методы решения нелинейных уравнений

Итерационные методы используются для решения нелинейных алгебраических и трансцендентных уравнений.

Уравнения в общем случае можно представить следующим образом:

f(x)=0.

Нелинейные уравнения можно разделить на два класса - алгебраические и трансцендентные.

Алгебраическими считаются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные).

Алгебраическое уравнение в общем виде можно представить многочленом n-й степени с действительными коэффициентами:

f(x)=a₀+a₁x+...+a_n-1x^n-1+a_n xⁿ=0 .

Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными, например: x³+x²+2e^x+5=0; 2x-sin3x=0.

Задача решения уравнения заключается в нахождении таких значений х, которые обращают его в тождество.

<3 4 567 8 9 >

Дата добавления: 2016-06-15; просмотров: 3441;

Поиск по сайту

Узнать еще