Кольцо многочленов с матричными коэффициентами.
Пусть P – поле, 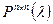 - кольцо многочленов с матричными коэффициентами. В силу не коммутативности кольца матриц возникают некоторые сложности с вычислением значения многочлена, делением многочленов. Соответственно определяется левое и правое значение многочлена (в зависимости с какой стороны записана переменная), а также левое и правое деление многочленов с остатком.
- кольцо многочленов с матричными коэффициентами. В силу не коммутативности кольца матриц возникают некоторые сложности с вычислением значения многочлена, делением многочленов. Соответственно определяется левое и правое значение многочлена (в зависимости с какой стороны записана переменная), а также левое и правое деление многочленов с остатком.
Теорема 6.4 (Обобщенная теорема Безу) Остаток деления многочлена  на двучлен
на двучлен 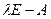 слева (справа) равен левому (правому) значению многочлена.
слева (справа) равен левому (правому) значению многочлена.
Доказательство. Нудновато
Теорема 6.5. Матрицы 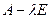 и
и 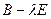 эквивалентны тогда и только тогда, когда матрицы
эквивалентны тогда и только тогда, когда матрицы 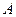 и
и 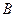 подобны.
подобны.
Доказательство. Пусть A и B подобны, то есть 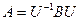 . Тогда
. Тогда 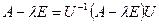 , матрица U – унимодулярная.
, матрица U – унимодулярная.
Пусть матрицы  и
и 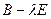 эквивалентны. Тогда найдутся унимодулярные матрицы
эквивалентны. Тогда найдутся унимодулярные матрицы 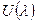 и
и 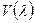 , что
, что 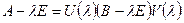 . Равенство запишем в виде
. Равенство запишем в виде 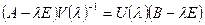 . Поделим многочлен
. Поделим многочлен 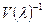 на
на 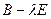 справа, а
справа, а 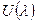 на
на  слева. Получим
слева. Получим 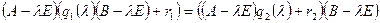 . Раскроем скобки, получим
. Раскроем скобки, получим 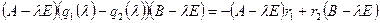 . Справа стоит многочлен степени не выше 1, значит
. Справа стоит многочлен степени не выше 1, значит  . Тем самым установлено равенство
. Тем самым установлено равенство 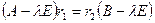 или
или 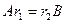 и
и 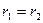 . Для доказательства подобия осталось показать невырожденность матрицы
. Для доказательства подобия осталось показать невырожденность матрицы 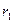 . Поскольку
. Поскольку  , то поделив
, то поделив 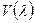 справа на
справа на  имеем
имеем 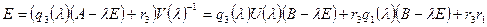 , и, значит,
, и, значит, 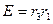 .
.
Дата добавления: 2016-07-27; просмотров: 1719;











