Присоединение корня многочлена.
Пусть P произвольное поле, P(x) - кольцо многочленов с коэффициентами из P. В кольце многочленов P(x) рассмотрим множество (f(x)) всех многочленов, делящихся без остатка на f(x). Множество (f(x)) образует двусторонний идеал. Элементами факторкольца P(x)/(f(x)) являются смежные классы. Каждый смежный класс состоит из тех и только тех многочленов, которые имеют одинаковый остаток от деления на f(x). Естественно, каждому смежному классу поставить многочлен наименьшей степени, который является остатком от деления всех многочленов этого класса на f(x). Пусть степень f(x) равна n. Тогда элементами факторкольца являются многочлены степени не выше n-1 с коэффициентами из P. Операции сложения и умножения в этом кольце сводятся к аналогичным операциям с остатками от деления на f(x).
Теорема 3.4. Факторкольцо P(x)/(f(x)) является полем тогда и только тогда, когда многочлен f(x) неприводим над полем P.
Доказательство. Если f(x) приводимый многочлен, то фактор кольцо содержит делители нуля, и, следовательно, не является полем. Пусть f(x) неприводимый многочлен. Для любого не нулевого многочлена g(x) степени меньше n НОД(f(x),g(x))=1, и, значит, найдутся такие многочлены u(x) и v(x), что u(x)f(x)+v(x)g(x)=1. Но тогда 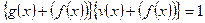 , то есть для любого не нулевого элемента существует обратный к нему.
, то есть для любого не нулевого элемента существует обратный к нему.
Пусть f(x) – неприводимый многочлен над полем P. Факторкольцо P(x)/(f(x)) является полем, и содержит все элементы поля P (точнее содержит подполе изоморфное P). Смежный класс {x+(f(x))} является корнем многочлена f(x). Действительно, при подстановке в f(x) получим смежный класс (f(x))=0. Таким образом, факторкольцо P(x)/(f(x)) кроме элементов P содержит корень многочлена f(x), и может рассматриваться как расширения поля P.
Пусть теперь f(x) произвольный многочлен. Разложим f(x) на неприводимые многочлены. Если хотя бы один из них имеет степень больше либо равную 2, то можно расширить исходное поле. Процесс расширения можно продолжать до тех пор, пока многочлен f(x) не будет разлагаться на линейные множители. Следовательно, любое поле P можно расширить до поля, в котором многочлен f(x) разлагается на линейные множители.
Гомоморфизм колец.
Однозначное отображение кольца K в кольцо H, сохраняющее операции сложения и умножения, называется гомоморфизмом колец ( 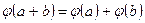 и
и 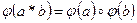 ).
).
Свойство 3.4. 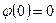 ,
, 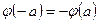 .
.
Множество элементов кольца K, образ которых равен 0, называют ядром гомоморфизма и обозначают 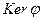 , а множество элементов H, для которых существует прообраз, называют множеством образов и обозначают
, а множество элементов H, для которых существует прообраз, называют множеством образов и обозначают 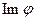 .
.
Свойство 3.5. 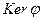 - двусторонний идеал в K
- двусторонний идеал в K
Доказательство. Пусть 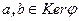 . Так как
. Так как 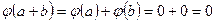 , то
, то 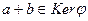 . Аналогично,
. Аналогично, 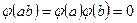 , и
, и 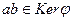 . Далее,
. Далее, 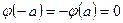 , то есть
, то есть 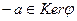 . Тем самым установлено, что
. Тем самым установлено, что 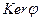 - подкольцо. Для
- подкольцо. Для 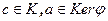 имеем
имеем 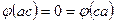 , то есть
, то есть 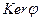 - двусторонний идеал в K.
- двусторонний идеал в K.
Свойство 3.6. 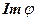 - подкольцо H
- подкольцо H
Доказательство. Пусть 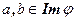 , тогда найдутся их прообразы c,d и так далее…
, тогда найдутся их прообразы c,d и так далее…
Теорема 3.5. Факторкольцо 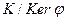 изоморфно
изоморфно 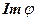 . Для любого двустороннего идеала I кольца K существует гомоморфизм с ядром равным I, например, в K/I.
. Для любого двустороннего идеала I кольца K существует гомоморфизм с ядром равным I, например, в K/I.
Доказательство. Изоморфизм задается соотношением 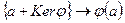 .
.
Дата добавления: 2016-07-27; просмотров: 2585;











