Численное дифференцирование.
Как правило, формулы численного дифференцирования применяются для вычисления производной таблично заданной функции вида 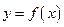 , либо для функций, вычислить производную которой аналитически слишком сложно.
, либо для функций, вычислить производную которой аналитически слишком сложно.
Суть численного вычисления производной сводится к замене исходной табличной функции 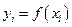 , где
, где 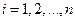 , приближающей функцией, которую можно легко вычислить. Чаще всего в роли приближающей функции выбирается интерполяционный многочлен
, приближающей функцией, которую можно легко вычислить. Чаще всего в роли приближающей функции выбирается интерполяционный многочлен 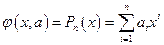 , в этом случае производные вычисляются дифференцированием многочлена. На практике, как правило, вычисляются производные 1-го и 2-го порядков.
, в этом случае производные вычисляются дифференцированием многочлена. На практике, как правило, вычисляются производные 1-го и 2-го порядков.
В качестве первого приближения функцию 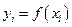 можно аппроксимировать отрезками прямой:
можно аппроксимировать отрезками прямой:
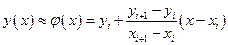 , тогда первую производную можно записать как:
, тогда первую производную можно записать как:
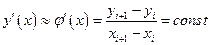 .
.
Рассмотрим случай аппроксимации функции с помощью многочлена, тогда имеем:
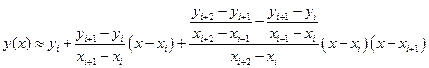 ,
,
формула для 1-ой производной:
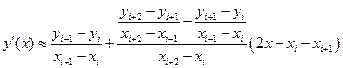 ,
,
формула для вычисления 2-ой производной:
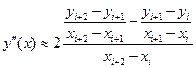 .
.
Применяя разделённые разности формулы численного дифференцирования могут быть записаны в виде:
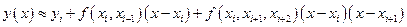 ,
,
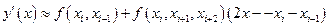 ,
,
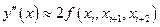 .
.
В случае равностоящих узлов, т.е. 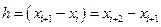 формулы численного дифференцирования примут вид:
формулы численного дифференцирования примут вид:
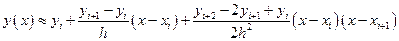 ,
,
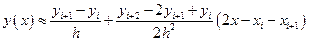 ,
,
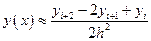 .
.
Дата добавления: 2020-10-25; просмотров: 499;











