Решение ОДУ методом Эйлера и уточнённым методом Эйлера

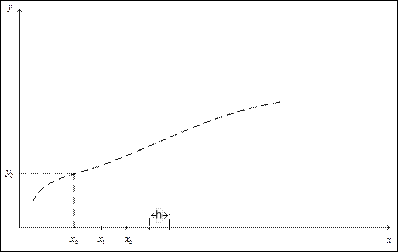
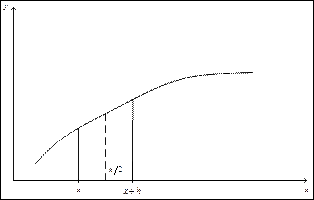
Представим искомую функцию 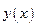в виде ряда Тейлора, предполагая, что она гладкая.

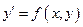
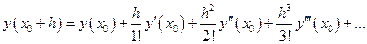
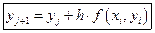
Любое ДУ (даже высокого порядка) с помощью преобразования и подстановки может быть приведён к виду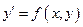

Метод Эйлера самый простой одношаговый метод им можно пользоваться для гладких функций.

Модифицированный метод Эйлера.

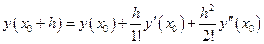
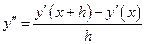
подставив вторую производную в ряд Тейлора, после преобразований получим формулу модифицированного метода Эйлера:

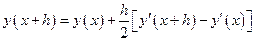
Задание на лабораторную работу №3

№1

Для ДУ 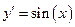найти первообразную и , восстановив её на интервале 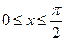, оценить локальные и глобальные ошибки в методе Эйлера при различном шаге интегрирования .

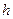Оценить минимальный шаг интегрирования 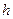, обеспечивающий глобальную ошибку не более .

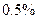№1

Выполнить задание №1 модифицированным методом Эйлера. Сопоставить два метода при равном шаге интегрирования.

Ввести в программы интегрирования программы оценки времени работы процессора. Сравнить методы.