Задача экстраполяции.
Задача интерполяции в некоторых случаях позволяет решить задачу экстраполяции - приближённое определение значений функции 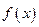 в точках
в точках 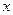 , лежащих вне отрезка
, лежащих вне отрезка 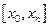 , по её значениям в точках
, по её значениям в точках 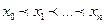 .
.
Задача аппроксимации таблично заданной функции (методы интегрального сглаживания).
Часто в функциях заданных таблично присутствуют случайные ошибки. Задача аппроксимации заключается в построении функции или нахождении функции являющейся наилучшим приближением по какому-либо критерию. Наиболее часто для этого использую метод наименьших квадратов.
Отличие от задачи интерполяции заключается в том, что в задачи аппроксимации нет математического обоснования, подтверждающего правильность решения.
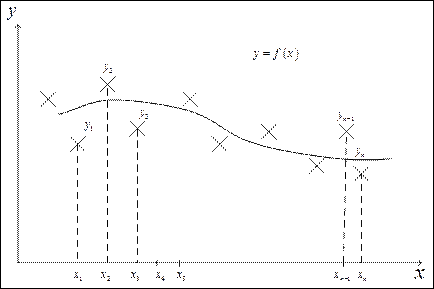
Задачи аппроксимации определяются моделью выбранной аппроксимирующей функции. Наиболее часто используется линейная модель на классе базисных функций.
На практике удобно представить искомую зависимость в виде обобщённого многочлена
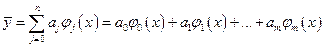 , где
, где 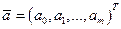 - вектор неизвестных коэффициентов,
- вектор неизвестных коэффициентов, 
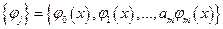 - заданная система базисных функций,
- заданная система базисных функций, 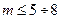 , при этом
, при этом 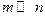 .
.
Дата добавления: 2020-10-25; просмотров: 604;











