Метод простой итерации.
Данный метод наиболее удобен с точки зрения организации процесса итерации. Он достаточно быстрый, но может быть расходящимся. Метод простой итерации базируется на преобразовании исходного уравнения 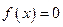 к виду
к виду  , при этом для сходимости итерационного процесса требуется выполнение условия
, при этом для сходимости итерационного процесса требуется выполнение условия 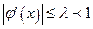 , где
, где  - некоторая константа.
- некоторая константа.
На втором этапе необходимо задать начальное приближение 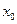 , принадлежащем интервалу нахождения корня, а также число
, принадлежащем интервалу нахождения корня, а также число 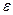 - заданную точность.
- заданную точность.
Вычисляем следующее приближение  . Повторяем итерационную процедуру пока
. Повторяем итерационную процедуру пока 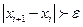 .
.
Задание на лабораторную работу №3
№1
организовать алгоритм нахождения корней квадратного уравнения методом простой итерации, оценить сходимость процесса итераций в зависимости от преобразования уравнения:

преобразование
1. 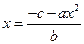
2. 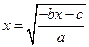 .
.
Тогда в преобразованном исходном уравнении можно получить оценку о сходимости итераций. Воспользуемся для преобразованного уравнения формулой Лагранжа и оценим поведение функции в окрестности произвольной точки 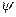 :
:
 , где
, где 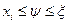
Если на функцию  наложить условие
наложить условие 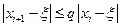 , то модули приращения будут зависеть от параметра
, то модули приращения будут зависеть от параметра  . Отсюда следует условие для преобразования исходного уравнения: правая часть уравнения должна иметь значение по модулю меньше единицы, т.е. производная правой части окрестности корня должна быть меньше единицы. Иначе итерационный процесс будет расходящимся.
. Отсюда следует условие для преобразования исходного уравнения: правая часть уравнения должна иметь значение по модулю меньше единицы, т.е. производная правой части окрестности корня должна быть меньше единицы. Иначе итерационный процесс будет расходящимся.

№2
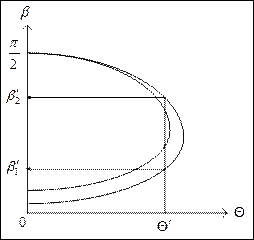
Для заданного числа Маха и угла поворота потока 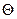 найти угол наклона косого скачка уплотнения
найти угол наклона косого скачка уплотнения 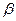 . Задачу решить двумя методами – методом деления пополам и любой подпрограммой из библиотеки IMSL. Сравнить потребное число итераций при одинаковом начальном
. Задачу решить двумя методами – методом деления пополам и любой подпрограммой из библиотеки IMSL. Сравнить потребное число итераций при одинаковом начальном 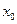 .
.
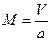 , где
, где 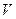 - скорость потока;
- скорость потока; 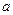 - скорость звука.
- скорость звука.

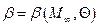
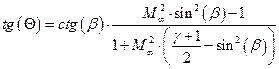 , где
, где 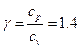 для воздуха.
для воздуха.
Данное трансцендентное уравнение имеет два вещественных корня 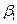 и
и 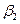 . В качестве нулевого приближения можно воспользоваться известными аналитическими решениями.
. В качестве нулевого приближения можно воспользоваться известными аналитическими решениями.
Если 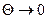 , то
, то 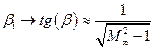 ,
, 
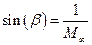 .
.
Точности нахождения корней 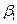 ,
, 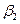 назначить следующие:
назначить следующие: 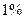 ,
, 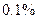 ,
, 
Дата добавления: 2020-10-25; просмотров: 478;











