Формула Адамса для предиктора и корректора.
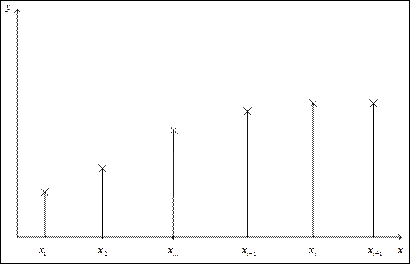
Для запуска многошагового метода расчёта «стартовых точек» используют одношаговые методы, т.е. рассчитывается необходимое количество 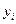 для запуска многошагового метода.
для запуска многошагового метода.
Идея метода Адамса достаточно проста:
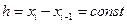
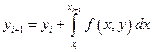
тогда значение функции в следующей точке можно записать через интеграл с помощью 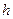 .
.
Если воспользоваться задачей интерполирования, то подынтегральную функцию можно представить в виде интерполяционного многочлена из условий прохождения его через 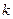 предыдущих точек.
предыдущих точек.
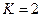
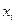
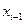
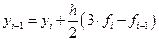
Чаще всего метод Адамса используют для 4-х точек
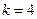
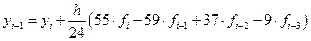
Используя прямой метод Адамса, мы решаем задачу предиктора по многочлену, проведённому через точки, мы экстраполируем значения функции.
Поскольку в математическую оценку для задачи экстраполяции получить практически невозможно, то для уточнения 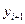 можно использовать интерполяционную процедуру корректора. Т.е. включить в расчёт значение найденного
можно использовать интерполяционную процедуру корректора. Т.е. включить в расчёт значение найденного 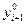 .
.
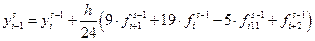
Многошаговые методы достаточно точные, и, если ДУ не имеет особенностей, требуемая точность достигается на более крупном шаге интегрирования по сравнению с одношаговыми методами.
Метод Рунге-Кутта
Если мы воспользуемся рядом Тейлора, то приращение функции 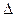 можно записать через коэффициенты ряда:
можно записать через коэффициенты ряда:
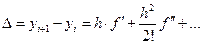
В методе Рунге-Кутта разницу приращений можно представить в виде функций 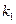 и
и 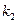 , если воспользоваться двумя точками:
, если воспользоваться двумя точками:
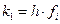 и
и 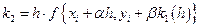
коэффициенты 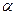 и
и 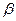 будут найдены из условий совпадения искомой функции
будут найдены из условий совпадения искомой функции 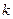 с соответствующими членами ряда Тейлора.
с соответствующими членами ряда Тейлора.
В общем виде можно получить обобщенное выражение для поиска функций 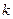 :
:
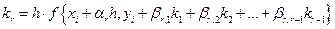 , где
, где 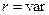 .
.
Таким образом, задаваясь различными 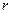 , получим рекуррентные формулы, являющиеся формулами Рунге-Кутта.
, получим рекуррентные формулы, являющиеся формулами Рунге-Кутта.
Наиболее часто в методе Рунге-Кутта используется метод 3-го и 4-го порядка:
Пример.
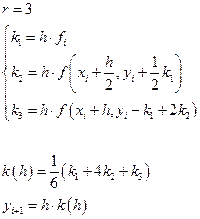
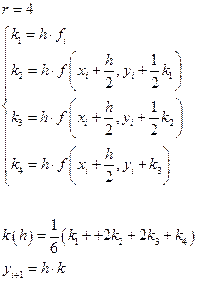
Дата добавления: 2020-10-25; просмотров: 513;











