Основные методы оптимизации в задачах специальности.

В задачах аэрогидромеханики формулируются задачи. Требующие так называемых оптимальных решений.

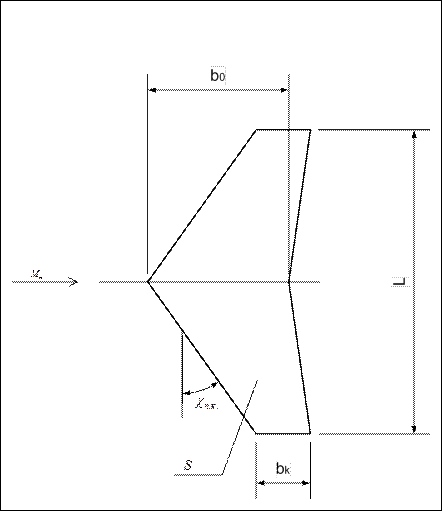
Параметры влияющие на аэродинамические характеристики крыла:

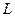- размах крыла;

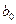- корневая хорда крыла;

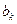- концевая хорда крыла

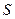- площадь крыла;

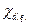- угол стреловидности крыла по передней кромке

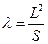- удлинение крыла;

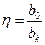- сужение крыла;

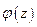- крутка;

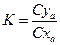- аэродинамическое качество,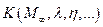

При решении вариационных задач оптимизации очень часто не существует функциональной зависимости (формул), связывающих функцию с параметрами (независимыми переменными).

Для численных расчётов значений оптимума искомой функции используют различные алгоритмы, отличающиеся быстродействием и точностью. Для решения задач оптимизации введём основные понятия и определения:

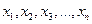- независимые переменные;

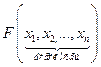- целевая функция.

Под словом «целевая» объединяют задачи «минимакса»:

,

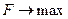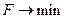
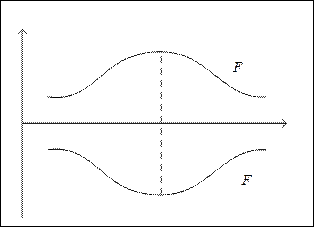
В задачах «минимакса» подразумевают 2 основных класса решения:

1. без ограничений;
2. с ограничением типа равенства и неравенства.

Говорят о поле поиска проектных параметров на подмножестве 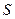, не имеющих границ. Однако в инженерных задачах на область 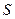чаще всего накладываются ограничения:

а) тип равенств

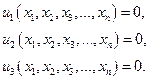
б) тип неравенств

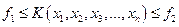
При решении задач оптимизации большинство численных методов предполагают важнейшее свойство целевой функции - 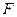-функция унимодальная. Мы считаем, что на множестве 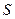функция 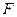имеет одно максимальное (минимальное) значение.

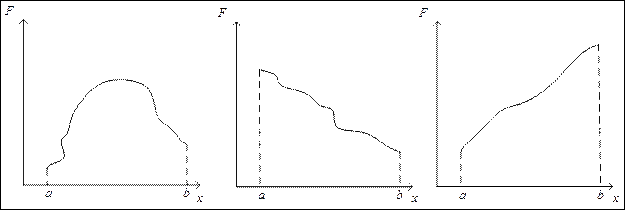
Как правило, проектные параметры всё-таки локализованы на некотором интервале поиска. Тогда говорят, что унимодальная функция имеет глобальный экстремум и может иметь достаточно много локальных экстремумов. Часто экстремум целевой функции может лежать на границах интервала поиска, а эти границы определены ограничениями типа равенств и неравенств.

Задача.

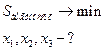
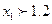
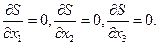
при решении задач на экстремум выбор алгоритма поиска оптимальных проектных параметров очень сильно зависит от целевой функции 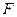. Для одних целевых функций данный алгоритм будет высокоэффективным, но для других целевых функций данный алгоритм может вовсе не найти существующие экстремумы.

Как показывает опыт решения экспериментальных задач – желательно найти экстремум несколькими численными методами. В общем случае все численные методы поиска, даже при простых алгоритмах, весьма трудоёмки. Принято говорить о так называемом кубе поиска.

Если отнормировать все проектные параметры:

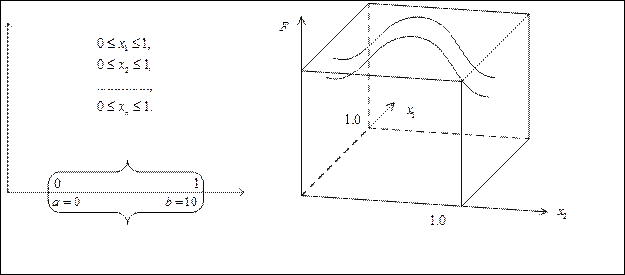
Также говорят о допустимом интервале поиска проектного параметра.

Для оценки алгоритмов поиска экстремума целевой функции будем рассматривать их на задачах одномерного поиска.

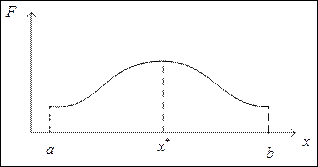
Предполагаем, что до запуска алгоритма мы по каким-то соображениям определили диапазон поиска.

Предполагаем, что функция унимодальная и алгоритм поиска обязан найти экстремум.