Метод наименьших квадратов.

Пусть у нас есть таблично заданная функция , 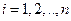. В значениях присутствуют случайные ошибки.

Требуется найти такие коэффициенты 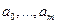, чтобы выполнялось интегральное условие согласования:

, тогда минимум будет достигаться, если

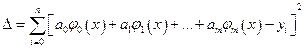
В этом случае условия безусловного экстремума примут вид

, , тогда придём к системе:

,

Задание на лабораторную работу №3

№1

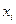
	0.2	0.3	0.5	0.8	1.2

Написать программу линейного интерполирования для таблично заданной функции с произвольным распределением аргумента. Проинтерполировать функцию , на интервале 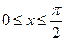при различном числе узлов.

, , .

№2

Проинтерполировать функцию задания №1 методом Лагранжа. Сравнить результаты с результатами полученными метолом линейной интерполяции.

Основные положения численных методов для решения обыкновенных дифференциальных уравнений (ОДУ).

Для решения ОДУ численными методами существуют алгоритмы, позволяющие находить первообразную на интересующем нас интервале аргумента, т.е. говорят о границе решения (левая, правая).

Задача Коши.

Пример. Решение ОДУ:

Говорят, что задача Коши – это решение ДУ при соответствующих начальных условиях задачи.

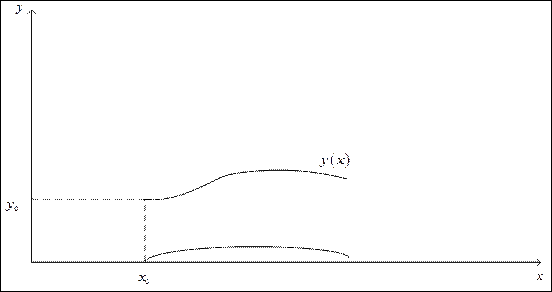
Для задачи Коши существует достаточно большое число алгоритмов нахождения 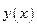, но все они подразделяются на одношаговые и многошаговые.

В многошаговых методах используется информация не только в 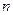-ой точке , но и в ряде предыдущих точек, вычисленных ранее. Но, поскольку, решается задача Коши для многошаговых методов приходиться рассчитывать начальные точки по одношаговому алгоритму.

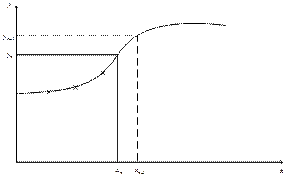
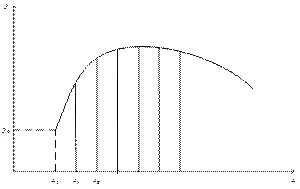
Для решения задачи Коши пользователь назначает требуемую точность решения. Если требуемая точность достаточно высока, то возможен случай, когда компьютер решения вовсе не найдёт.

Ни один численный алгоритм решения ОДУ не может обеспечить точность решения, стремящуюся к аналитическому решению.

В численном решении всегда существует два типа ошибок: ошибка округления и ошибка дискретизации. Большинство методов используют представление искомой функции либо в виде рядов, либо в виде специальных функций, но это представление 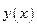всегда конечно. Если используются алгоритмы рядов, то всегда можно оценить (приближённо) ошибку дискретизации и назначить соответствующий шаг интегрирования.

В ходе решения ОДУ подразделяют ошибки в решении на локальную и глобальную. Локальная – ошибка при вычислении конкретного решения 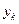в какой-то точке. В сумме все локальные ошибки приведут к накоплению глобальной ошибки, поэтому при решении не надо «увлекаться» и расширять интервалы интегрирования.