Численное интегрирование

Необходимость вычисления значений определенных интегралов при моделировании возникает достаточно часто.

Формула Ньютона-Лейбница 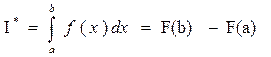(6.1)

имеет ограниченное применение:

· во-первых, не позволяет вычислить интегралы от таблично заданной подынтегральной функции f(x);

· во-вторых, не всякая подынтегральная функция имеет первообразную F(x).

Численные методы интегрирования универсальны: позволяют вычислить значение определенного интеграла непосредственно по значениям подынтегральной функции f(x), независимо от способа ее задания или вида аналитического выражения.

Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x), и прямыми x=a и x=b (Рис.6.1.).

Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются квадратурными (формулами вычисления площади).

Рассмотрим получение и применение простейших формул.

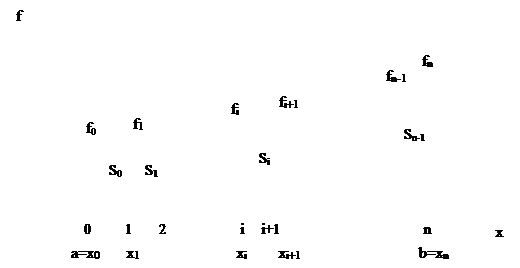
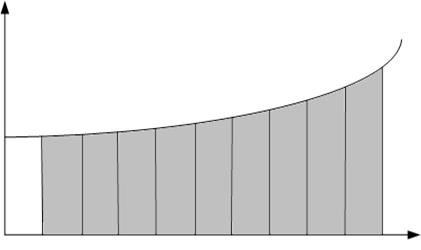
Рис. 6.1. Геометрический смысл определённого интеграла

Отрезок [a, b] делят на n необязательно равных частей – элементарных отрезков. Принято такое деление отрезка называть сеткой, а точки x₀, x₁,…, x_n – узлами сетки.

Если сетка равномерная, то 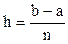– шаг сетки, при интегрировании – шаг интегрирования, а координата i-го узла вычисляется по формуле:

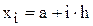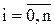, (6.2)

Полная площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций – элементарных площадей:

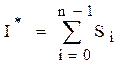(6.3)

Квадратурные формулы отличаются друг от друга способом оценки значения S_i – площади элементарной криволинейной трапеции.

Рассмотрим получение простейших формул для часто используемой равномерной сетки.

6.1. Формулы прямоугольников

Площадь i-той элементарной трапеции можно оценить (приближенно вычислить) как площадь прямоугольника со сторонами 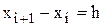и f_i. Тогда 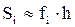и значение интеграла:

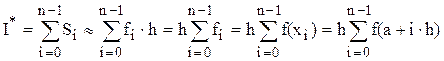(6.4)

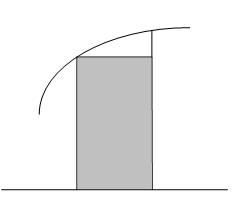
Рис. 6.2. Оценка элементарной площади S_i левым прямоугольником.

Полученная формула называется формулой левых прямоугольников, т.к. для оценки площади использовалось левое основание элементарной криволинейной трапеции.

Аналогично можно получить формулу правых прямоугольников:

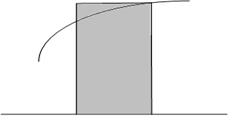
Рис. 6.3. Оценка элементарной площади S_i правым прямоугольником.

Для данного случая 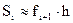и тогда значение интеграла:

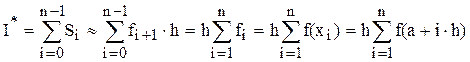(6.5)

Эти формулы не находят широкого применения, т.к. имеют большую погрешность, пропорциональную величине шага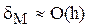

Как появляется эта погрешность, видно на рисунках.

Для повышения точности площадь S_i можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка

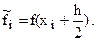
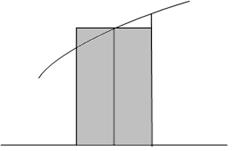
Рис. 6.4. Оценка элементарной площади S_i средним прямоугольником.

Для данного случая 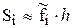и формула средних прямоугольников имеет вид:

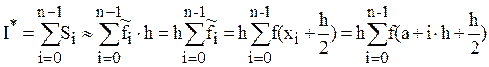(6.6)

Как видно из рис. 6.4, погрешность в оценке площади S_i в данном случае существенно меньше, чем в двух предыдущих (погрешность оценивается разницей площадей δ₁ и δ₂).

Погрешность метода пропорциональная квадрату величины шага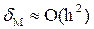

Схема алгоритма вычисления значения определённого интеграла по приведённым квадратурным формулам представлена на рис. 6.6.

Пример 6.1. Вычисление значения определённого интеграла по формулам прямоугольников. Для упрощения ручных расчетов рассмотрим достаточно простую задачу.

Требуется вычислить:

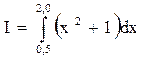
Точное значение легко вычисляется по формуле Ньютона-Лейбница:

=

=

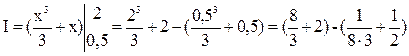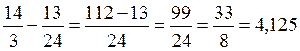
Для вычисления интеграла по квадратурной формуле необходимо выбрать число узлов n.

Пусть n=5, тогда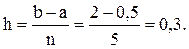

Расчет по формуле левых прямоугольников:

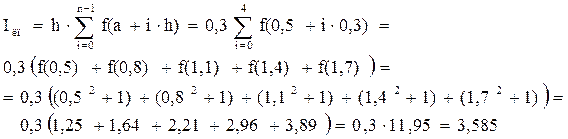
Погрешность расчета .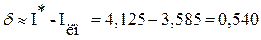

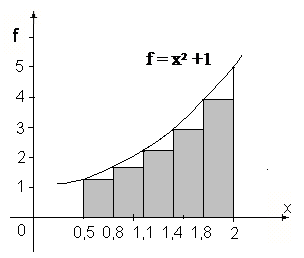
Суммарная площадь прямоугольников заметно меньше площади криволинейной трапеции.

Знак и значение погрешности можно легко оценить по геометрической иллюстрации вычисления интеграла по квадратурной формуле.

Рис. 6.5. Геометрическая иллюстрация вычисления значения определённого интеграла по формуле левых прямоугольников.

Расчет по формуле правых прямоугольников:

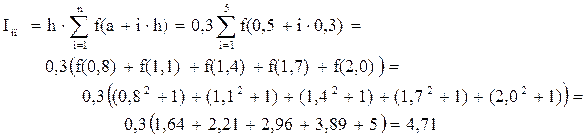Погрешность расчета d » 4,125 - 4,71 = - 0,585.

Для повышения точности необходимо увеличить n или использовать более точные квадратурные формулы.

Расчет по формуле средних (центральных) прямоугольников:

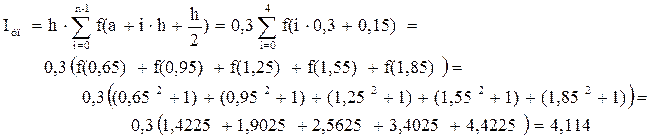Погрешность расчета d » 4,125 - 4,114= 0,011.

Формула средних прямоугольников на порядок точнее предыдущих формул.

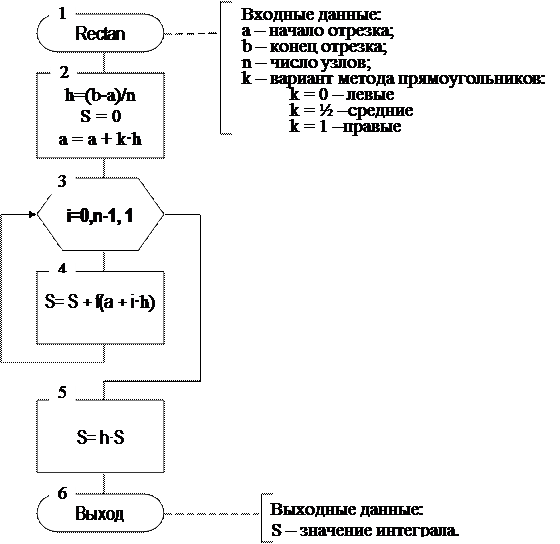Рис. 6.6. Схема алгоритма метода прямоугольников.

6.2. Формула трапеций

В данном методе элементарная криволинейная трапеция заменяется трапецией (кривая f(x) заменяется хордой CD).

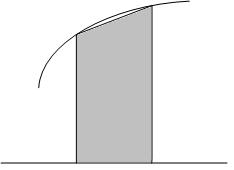Рис. 6.7. Оценка элементарной площади S_i трапецией.

Из рисунка видно, что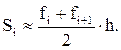

Отсюда:

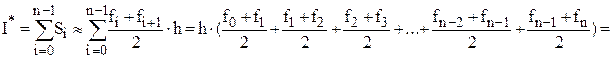
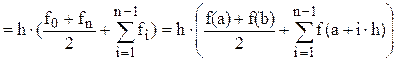(6.7)

Погрешность формулы трапеций пропорциональная квадрату шаг h 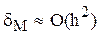т.е. формулы центральных прямоугольников и трапеций имеют близкую точность.

Пример 6.2. Вычислить по формуле трапеций значение ранее рассмотренного определённого интеграла 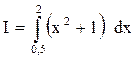при n =5, h = 0,3.

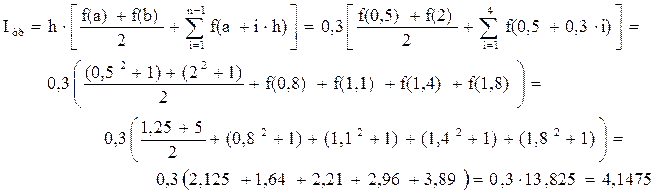Погрешность расчета d » 4,125 – 4,1475.

Формула трапеций имеет такую же точность, как и формула центральных прямоугольников.

Знак погрешности легко объяснить по геометрической иллюстрации применения формулы.

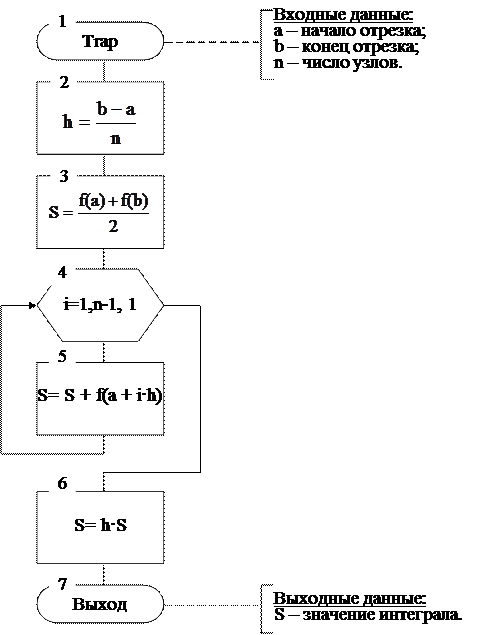Рис. 6.8. Схема алгоритма метода трапеций.

6.3. Формула Симпсона

На каждом элементарном отрезке подынтегральная функция f(x) заменяется квадратичной параболой, построенной по трем точкам: концам элементарного отрезка ( 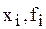), ( ) 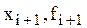и его середине ( ).

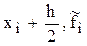Площадь полученной криволинейной трапеции служит оценкой элементарной площади S_i:

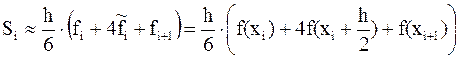
Тогда значение интеграла:

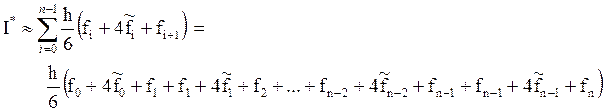
Добавим в скобки 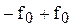, вынесем общий множитель за скобки:

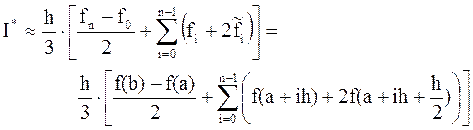(6.8)

Формула Симпсона имеет высокую точность, так как погрешность метода d_м = О(h³)

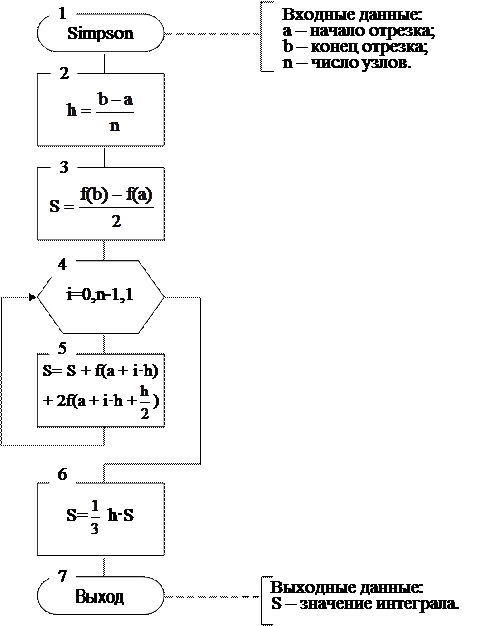Рис 6.9. Схема алгоритма метода Симпсона.

Пример 6.3. Вычисление значения ранее рассмотренного интеграла 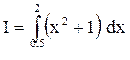по формуле Симпсона:

Для упрощения расчета возьмем n=2, тогда h=0,75.

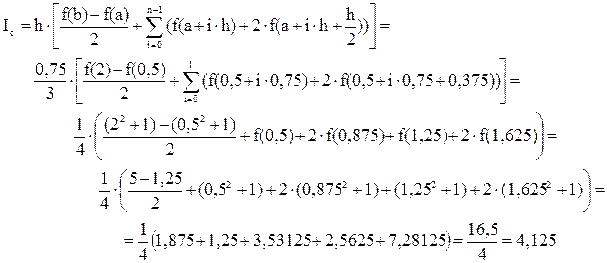
Погрешность расчета d = 4,125 – 4,125 = 0.

Такой результат объясняется тем, что подынтегральная функция в примере является квадратичной параболой, и замена ее параболой не вносит погрешности метода, а погрешность округления в расчётах отсутствует.

Рассмотренные формулы являются частным случаем формулы Ньютона-Котеса, полученной в общем виде при замене подынтегральной функции f(x) полиномом k-ой степени (при k=1 – формула трапеций, при k=2 – формула Симпсона). Чем больше k, тем точнее вычисляется интеграл при одинаковом числе узлов n.

Формула Симпсона получила название в честь британского математика Томаса Симпсона (1710—1761).

6.4. Выбор шага интегрирования.

При вычислении значения определенного интеграла от функций, заданных аналитически, необходимо обеспечить требуемую точность расчета ε. Точность вычисления можно повысить двумя способами:

1. Использовать более точную квадратурную формулу.

2. Увеличить количество узлов, соответственно уменьшить шаг интегрирования h.

Рис. 6.10. Схема алгоритма вычисления определенного интеграла

с автоматическим выбором шага интегрирования.

На практике обычно используется формула Симпсона, а требуемая точность расчета достигается вторым из указанных выше способов. Выполняется расчет с выбранным числом узлов n, затем выполняется расчет с удвоенным их числом. Если результаты отличаются более чем на требуемую точность, число узлов вновь удваивается. Расчет заканчивают, когда 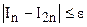, полагая, что 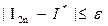, т.е. последнее вычисленное приближенное значение интеграла отличается от точного значения не больше чем на заданную точность. Такой способ называется автоматическим выбором шага интегрирования и легко реализуется на ЭВМ.

Начальный шаг интегрирования рекомендуется выбирать из соотношения:

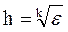
где k = 1 для формул правых и левых прямоугольников;

k = 2 для формул трапеций и центральных прямоугольников;

k = 3 для формулы Симпсона.

Важно напомнить, что погрешность решения включает погрешности метода δ_M и погрешность округления δ_O. При увеличении числа узлов n δ_M уменьшается, но растет δ_O, т.к. увеличивается количество арифметических действий для решения задачи. Зависимость этих величин показана на графике.

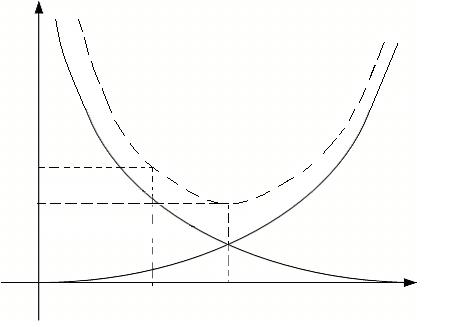
Рис. 6.11. Структура погрешности численного интегрирования.