Численное дифференцирование

 

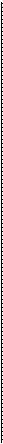Задача приближенного вычисления производной мо­жет возникнуть в тех случаях, когда неизвестно анали­тическое выражение для исследуемой функции. Функ­ция может быть задана таблично, или известен только график функции, полученный, например, в результате показаний датчиков параметров технологического про­цесса.

Иногда, при решении некоторых задач на компьюте­ре, из-за громоздкости выкладок может оказаться более удобным вычисление производных численным методом, чем аналитическим. При этом, разумеется, необходимо обосновать применяемый численный метод, т. е. убедить­ся в том, что погрешность численного метода находится в приемлемых границах.

Одним из эффективных методов решения дифференци­альных уравнений является разностный метод, когда вместо искомой функции рассматривается таблица ее значений в определенных точках, при этом производные приближенно заменяются разностными формулами.

5.1.Графическое дифференцирование

Пусть известен график функции у = f(х) на отрезке [а,b].Можно построить график производной функции, вспомнив ее геометрический смысл. Воспользуемся тем фактом, что производная функции в точке х равна тан­генсу угла наклона к оси абсцисс касательной к ее графи­ку в этой точке.

Если х = х0,найдем у0 = f(x0)с помощью графика и затем проведем касательную АВ к графику функции в точке (х0, y0) (рис. 5.1). Проведем прямую, параллельную касательной АВ, через точку (-1, 0) и найдем точку у1ее пересечения с осью ординат. Тогда значение у1равно тан­генсу угла наклона касательной к оси абсцисс, т. е. про­изводной функции f(x)в точке х0:

у1 = 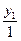= tgα = f ¢(x0), и точка М0 (х0, у1) принадлежит графику производной.

 

 

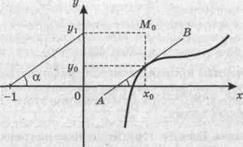
Рис. 5.1

Чтобы построить график производной, необходимо разбить отрезок [а, b]на несколько частей точками хi, затем для каждой точки графически построить значение производной и соединить полученные точки плавной кри­вой с помощью лекал.

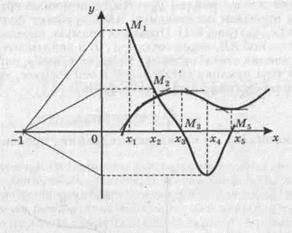
На рис. 5.2 показано построение пяти точек М1, М2,... , М5и графика производной.

Алгоритм построения графика производной:

1. Строим касательную к графику функции у = f(x)в точке (х1, f(x1));из точки (-1, 0) параллельно касатель­ной в точке (х1, f(x1)) проведем прямую до пересечения с осью ординат; эта точка пересечения дает значение про­изводной f ¢(х1).Строим точку М1(х1, f ¢(х1)).

2. Аналогично построим остальные точки М2, М3, М4и М5.

3. Соединяем точки М1, М2, М3, М4, М5плавной кривой.

M4

 

Рис. 5.2

Полученная кривая является графиком производной.

Точность графического способа определения производ­ной невысока. Мы приводим описание этого способа толь­ко в учебных целях.

Замечание. Если в алгоритме построения графика производ­ной вместо точки (-1, 0) взять точку (-l,0), где l > 0, то график будет построен в другом масштабе по оси ординат.

5.2.Разностные формулы

а) Разностные формулы для обыкновенных производных

Разностные формулы для приближенного вычисления производной подсказаны самим определением производной. Пусть значения функции в точках xi обозначены через yi:

yi = f(xi), xi = a+ ih, i = 0, 1, ... , n; h =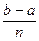

Мы рассматриваем случай равномерного распределения точек на отрезке [a, b]. Для приближенного вычисления производных в точках xi можно использовать следующие разностные формулы, или разностные производные.

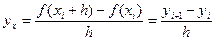. (5.1)

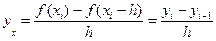. (5.2)

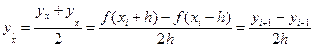. (5.3)

 

Так как предел отношения (5.1) при h ® 0 равен пра­вой производной в точке хi, то это отношение иногда на­зывают правой разностной производнойв точке xi.По аналогичной причине отношение (5.2) называют левой разностной производнойв точке xi.Отношение (5.3) на­зывают центральной разностной производнойв точке xi.

Оценим погрешность разностных формул (5.1)–(5.3), предполагая, что функция f(x) разлагается в ряд Тейло­ра в окрестности точки xi:

f(x) = f(xi)+ 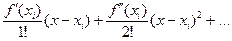. (5.4)

Полагая в (5.4) х = xi + h или х = хi - h, получим

yi+1 = f(xi + h) = yi + 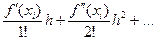. (5.5)

yi-1 = f(xi - h) = yi - 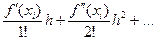. (5.6)

Учитывая (5.5) и (5.6), имеем

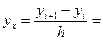
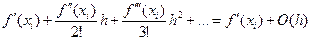, (5.7)

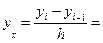
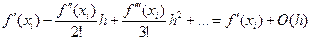, (5.8)

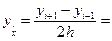
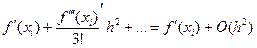. (5.9)

Из последних соотношений следует, что разностная формула (5.3) имеет погрешность на порядок меньшую, чем разностные формулы (5.1) и (5.2).

Производные высших порядков можно приближенно вычислять по формулам, полученным с помощью после­довательного применения разностных соотношений (5.1)–(5.3).

Разностная формула для второй производной (разно­стная производная второго порядка)имеет вид

 

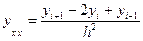. (5.10)

 

Непосредственной подстановкой разложений (5.5) и (5.6) в формулу (5.10) можно получить зависимость между второй производной функции и разностной формулой для производной второго порядка:

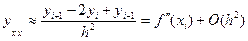. (5.11)

б) Разностные формулы для частных производных

Разностные формулы для частных производных ана­логичны формулам (5.1)–(5.3), (5.10).

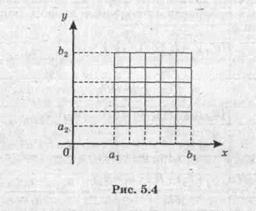
Пусть функция двух переменных и = f(x, у)определе­на в прямоугольной области а1£ х £ b1, а2£ у£ b2.

 

Определение 5.1.Назовем сеточной областьюмноже­ство точек (xi, yj),где

xi = a1+ ih1, i = 0, 1, ... , n1; h1= (b1 - a1)/n1,

yj = a2 + jh2, j = 0, l, ... , n2; h2 = (b2 - a2)/n2.

На рис. 5.4 изображена сеточная область для п1= 5, п2 = 5, которая состоит из 36 точек.

Введем обозначение uij = f(xi, yi).

Тогда для частных производных первого и второго порядка по переменной х можно записать разностные формулы (5.1)–(5.3) и (5.10):

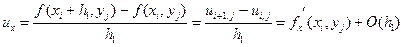. (5.12)

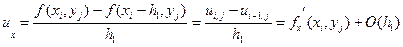. (5.13)

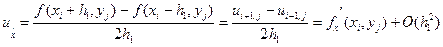. (5.14)

 

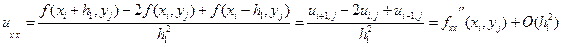(5.15)

Аналогичные разностные формулы можно записать и для частных производных первого и второго порядка по переменной у:

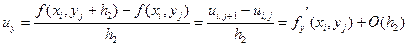. (5.16)

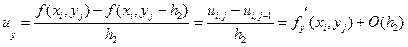. (5.17)

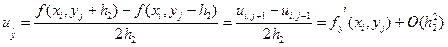. (5.18)

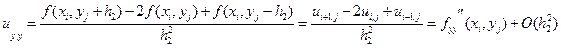(5.19)

 

Запишем разностные формулы для смешанных производных:

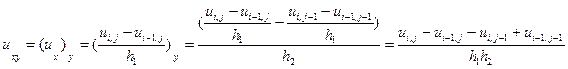(5.20)

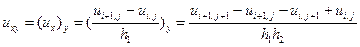(5.21)

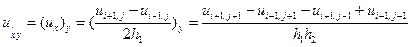(5.22)

 

5.3. Вычисление производных с помощью интерполяционных формул

Разностные формулы для производных не подходят в тех случаях, когда необходимо вычислить производную в произвольной точке, не совпадающей с узлами xi.В этих случаях естественно воспользоваться интерполяционны­ми формулами.

а) Равномерное распределение узлов

Пусть заданы значения функции yi = f(xi)в узлах хi,равномерно распределенных на отрезке [а, b]:

xi = а + ih, i = 0, 1,..., n; h = (b - a)/n.

Построим формулы приближенного дифференцирова­ния с помощью первой интерполяционной формулы Нью­тона(4.13), которую после некоторых упрощений мож­но записать в виде

Рn(х) = y0+ qóy0+ 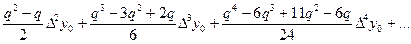, (5.23)

где q = (x – x0)/h.

Мы предполагаем, что узлы интерполяции распреде­лены на отрезке [а, b]равномерно с шагом h.

Выберем в качестве х0узел, ближайший к точке х. Дифференцируя (5.23) по переменной х и учитывая, что

,

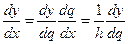получим приближенные формулы для вычисления про­изводных:

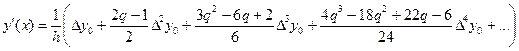, (5.24)

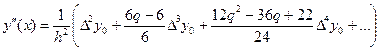. (5.25)

Чем больше слагаемых в формулах (5.24) и (5.25) ис­пользуется, тем выше точность вычисления производ­ных. Эти формулы дают хорошие приближения для то­чек, близких к значению х0(левому концу отрезка [а, b]).

Если х = х0,то q = 0 и для вычисления производных в узлах xi получим формулы

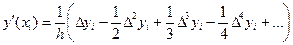, (5.26)

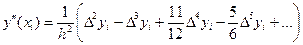. (5.27)

Очевидно, что вторая интерполяционная формула Ньютонапозволяет вывести формулы для вычисления производных в точках, близких к правому краю хn отрез­ка [а, b]:

 

Рn(х) = yn+ qóyn-1+ 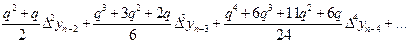, (5.28)

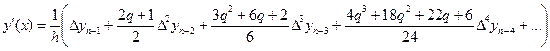, (5.29)

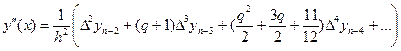. (5.30)

При x = xn получим

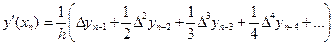, (5.31)

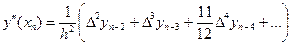. (5.32)

Выведем формулы для вычисления производной с по­мощью интерполяционного многочлена Лагранжа:

Ln(x) = × ,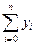

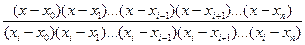y(x) = Ln(x) +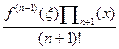

В случае равномерного распределения узлов с помо­щью обозначений

q = 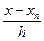, q[n+1] = q(q -1)...(q - n)

получим

Пn+1(x) = (х - х0)(х – х1) ...(х - хп) = hn + 1q(q -1)...(q-n) = hn+1 q[n+1],П׳n+1(xi) = (хi - х0)(хi – х1) ...(хi - хп) = hni(i-1)...1 (-1)...(-n+i) = (-1)n-1hni!(n-i)!.

Тогда полином Лагранжа запишем в виде

Ln(x) = .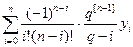

Найдем производную

y׳(x) = L׳n(x) = 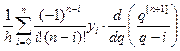. (5.33)

С помощью (5.33) получим формулы для вычисления производной в точках xi при различных значениях п:

1) п = 2. Используются три точки, и производная в
этих точках выражается формулами

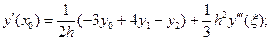
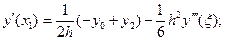(5.34)

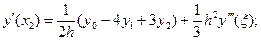
2) n = 3 (четыре точки).

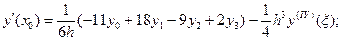
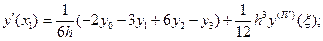(5.35)

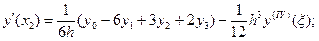
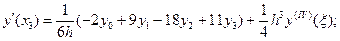
3) n = 4 (пять точек).

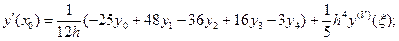
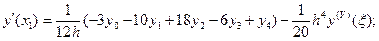
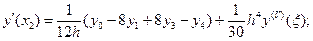(5.36)

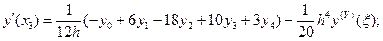
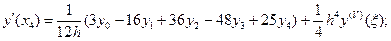
б) Неравномерное распределение узлов

Пусть известны значения yi функции в узлах хi:

x0 < x1 <x2 <...< xn-1 <xn.

В этом случае для вычисления производных использу­ют интерполяционный многочлен. Предположим, что точка х расположена ближе к начальному узлу х0,тогда мы можем применить первый интерполяционный много­член Ньютона

y(x) = y(x0) +(x - x0)y(x0, x1) + (x - x0)(x - x1)y(x0, x1, x2) + (x - x0)(x - x1)(x - x2)y(x0, x1, x2, x3) + ...

Здесь использованы обозначения для разделенных раз­ностей:

,

,

,...

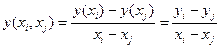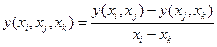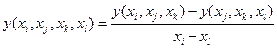Обозначим через 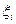разность (х - xi)и запишем много­член Ньютона в виде

y(x) = y(x0) + ξ0y(x0, x1) + ξ0ξ1y(x0, x1, x2) + ξ0ξ1ξ2y(x0, x1, x2, x3) + ... (5.37)

Теперь можем вывести формулы для производных:

у'(х) = у(х0, х1) + (ξ0 + ξ1)у(х0, х1, х2) + (ξ0ξ1+ ξ1ξ2 + ξ0ξ2) y(x0, x1, x2, x3) + ...

у"(х) = 2 y(x0, x1, x2) + 2(ξ0 + ξ1 + ξ2) y(x0, x1, x2, x3) + ...

y(k)(x) = k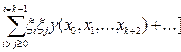![y(x0, x1, ..., xk) + (ξ0 + ξ1 +...+ ξk)y(x0, x1, ..., xk+1) +

+ (5.38)

Оставляя в (5.38) несколько слагаемых, получим фор­мулы для приближенного вычисления производных. При этом порядок погрешности по отношению к шагу разбие­ния h равен числу оставленных членов, или разности меж­ду числом узлов интерполяции и порядком производной.

Приведем некоторые простые формулы (h = max hi):

1. Первая производная по двум точкам:

y'(x) = y(x0, x1) + O(h) = 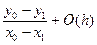(5.39)

Первая производная по трем точкам:

,

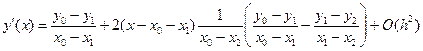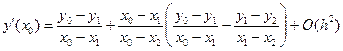, (5.40)

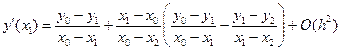
2. Вторая производная по трем точкам

 

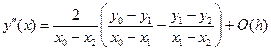(5.41)

 

Вторая производная по четырем точкам:

[

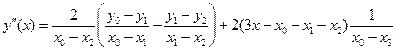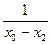
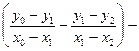
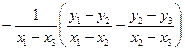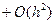] . (5.42)

Третья производная по четырем точкам:

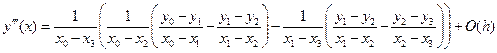. (5.43)

 

5.4. Практическая оценка погрешности. Метод Рунге-Ромберга

(Рунге Карл Давид Тольме(30.8.1856–3.1.1927) – немецкий физик и математик)

Рассмотрим метод Рунге для повышения порядка точ­ности формул для вычисления производных на примере формулы (5.11):

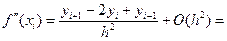
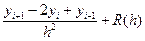(5.44)

Предполагая, что функция f(x)четырежды дифферен­цируема, погрешность разностной формулы для второй производной можно представить в виде

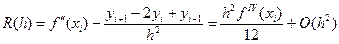(5.45)

Вычислим по формуле (5.44) вторую производную в той же точке хi, но используя сетку с шагом k·h, k – целое, например с k = 2:

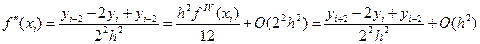(5.46)

 

Погрешность формулы (5.46) имеет вид

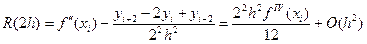(5.47)

Вычитая (5.45) из (5.47), получим

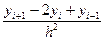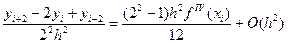- (5.48)

Отсюда для погрешности получим первую формулу Рунге:

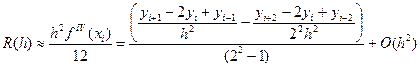(5.49)

Теперь вторую производную в точке xi можно вычис­лить по уточненной формуле (второй формуле Рунге):

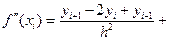
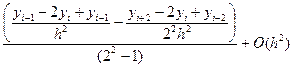(5.50)
<== предыдущая лекция | следующая лекция ==>
Приближение функций | Численное интегрирование

Дата добавления: 2020-08-31; просмотров: 414;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.038 сек.