Вторая задача динамики

По заданной массе и действующей на точку силе можно определить уравнения движения этой точки.

Рассмотрим решение этой задачи в декартовой системе координат. В общем случае сила 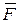является функцией многих переменных. Проецируя (1.2) на декартовы оси, получим

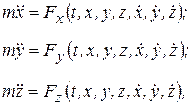(1.5)

если рассматривать случай зависимости силы только времени, координат и скорости.

Законы движения материальной точки представляют собой систему трех линейных дифференциальных уравнений второго порядка относительно неизвестных функций х(t), у(t), z(t), где независимым параметром является время t.

Общий интеграл этих уравнений содержит шесть произвольных постоянных. Функции, удовлетворяющие дифференциальным уравнениям движения точки и содержащие шесть произвольных постоянных интегрирования, называются общим решением дифференциальных уравнений движения свободной точки и записываются в виде

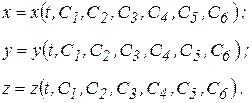
В каждой конкретной задаче постоянные интегрирования определяются из начальных условий задачи:

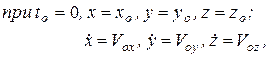(1.6)

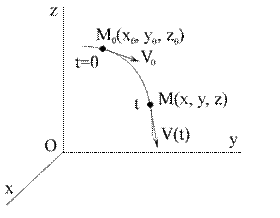Рис. 1.5

где 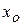, , 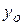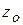- координаты движущейся точки; 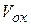, , 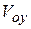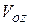- проекции ее скоростей (рис. 1.5).

Подчинив найденные первые и вторые интегралы дифференциальных уравнений (1.5) начальным условиям задачи (1.6), вычисляют все шесть постоянных интегрирования. Начальные условия задачи определяют единственное решение системы дифференциальных уравнений.

Интегрировать уравнения движения (1.5) можно с помощью определенных интегралов. Тогда нижние пределы интегрирования будут соответствовать значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, верхние пределы интегрирования будут соответствоватьзначению интегрируемых величин при текущем времени t.