Задача линейной интерполяции.
При построении линейной интерполяции предполагают, что на каждом интервале реальную функцию можно заменить отрезком прямой.
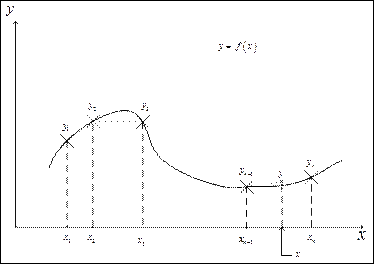
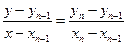
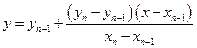
Линейная интерполяция – наиболее простой способ. При достаточно большом значении 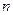 он может дать вполне приемлемую точность.
он может дать вполне приемлемую точность.
Линейная интерполяция как наиболее простой метод можно использовать для интерполирования функций с большим числом переменных (для экономии времени). Однако для функций с большими производными линейная интерполяция приводит к большим ошибкам, поэтому в задачах интерполяции чаще всего используют представление функции в виде многочленов.
Метод Лагранжа.
Наиболее удобным многочленом интерполяции является полином Лагранжа.
Пусть задано множество точек 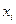 ;
; 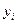 . Будем строить интерполяционную функцию в виде многочлена с пока неизвестными коэффициентами.
. Будем строить интерполяционную функцию в виде многочлена с пока неизвестными коэффициентами.
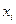 ;
; 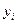
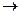
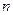
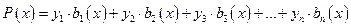
Если общий многочлен 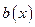 должен проходить через узловые точки
должен проходить через узловые точки 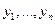 , мы придём к системе линейных уравнений относительно неизвестных коэффициентов:
, мы придём к системе линейных уравнений относительно неизвестных коэффициентов:
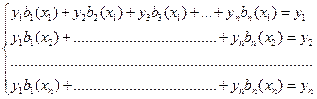
Однако условие прохождения через узлы требует единственности решения СЛАУ, чтобы все многочлены (лагранжевы многочлены влияния) отвечали условию:
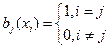
тогда для многочлена 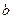 мы имеем выражение вида:
мы имеем выражение вида:
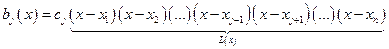
Таким образом вид многочлена 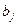 определён, по неизвестной константе
определён, по неизвестной константе 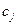 . Если
. Если 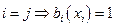
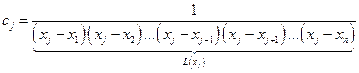
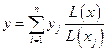
Дата добавления: 2020-10-25; просмотров: 533;











