Вероятностный анализ рискообразующих факторов в организационных задачах судоремонта

В последние годы, вследствие отсутствия государственных заказов на постройку судов, в деятельности судостроительных предприятий наметилась тенденция к выполнению судоремонтных работ [6, 7].

Процесс судоремонта представляет собой сложный технологический процесс, подверженный влиянию достаточно большого числа рискообразующих факторов: стоимость ремонтных работ, сроки продолжительности ремонта, качество ремонта, наличие необходимых производственных мощностей и персонала и ряд других.

Это выдвигает задачи анализа, прогнозирования и предвидения воздействия перечисленных факторов с целью эффективного решения ряда организационных мероприятий предшествующих непосредственному выполнению судоремонтных работ. Так, например, при принятии решения на заключение контракта, судовую компанию (Заказчик), прежде всего, будут интересовать такие факторы, как стоимость ремонтных работ, сроки продолжительности, качество ремонта и др. С другой стороны, судостроительное (судоремонтное) предприятие (Исполнитель) перед принятием решения о выполнении ремонтного заказа, должно оценить свои возможности в плане наличия необходимых производственных мощностей и персонала, запасов необходимых материалов и комплектующих изделий, нормативно-технической документации, необходимость привлечения контрагентов и др.

Для принятия решений в условиях риска могут использоваться модели, представленные деревьями вероятностей, на которых решаются задачи вероятностного вывода [9]. Предварительно каждый рискообразующий фактор, представляющий систему случайных событий, графически отображается в форме дерева распределения (рис. 2.5). Каждая ветвь дерева распределения отображает одно случайное событие и вероятность (р) его осуществления.

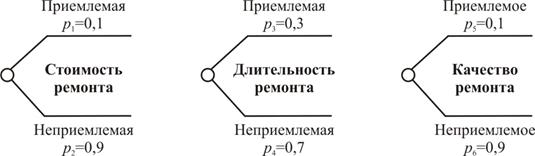
Рис. 2.5. Деревья распределений систем случайных рискообразующих событий

Комбинации таких деревьев, полученные их объединением, приводят к дереву вероятностей (рис. 2.6), которое представляет собой древовидный граф.

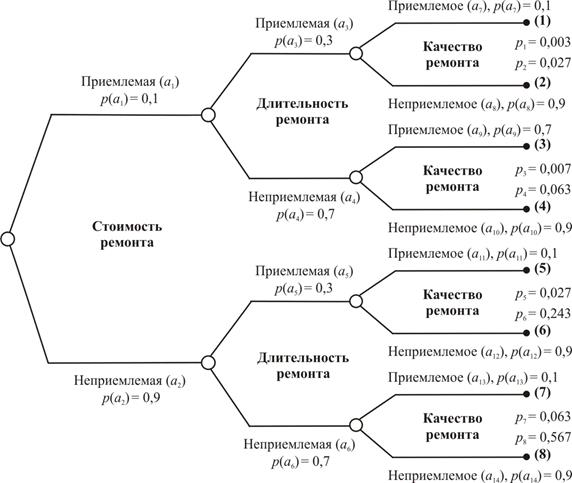
Рис. 2.6. Дерево вероятностей случайных рискообразующих событий при заключении контракта на выполнение судоремонтных работ

Каждый узел (вершина) такого графа связан с одной полной системой случайных событий. Каждое событие и вероятность его осуществления отображается ветвью дерева, выходящей из соответствующего узла. Каждый путь на дереве от корневого узла до конечной позиции отображает одну из возможных комбинаций событий, которая называется сценарием.

Дерево вероятностей на рис.2.6 представляет 8 возможных сценариев (обозначены на рис. последовательностью цифр в скобках).

Поскольку каждый сценарий образует одна возможная комбинация событий, по одному из каждой полной системы событий, общее число сценариев может быть подчинено ещё до конструирование дерева вероятностей как

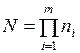, (2.8)

где n_i – число событий в i-ой системе; m – общее число систем случайных событий.

Вероятности осуществлении событий могут быть получены двумя способами: объективным (эмпирическим) и субъективным (экспертным). Первые из них получают с применением частотного подхода, который заключается в получении частотного от деления числа равновозможных исходов (n), благоприятствующих реализации интересующих событий на общее число равновозможных событий (N). При этом используется информация о прошлых реализациях событий за длительный период времени. Субъективные оценки вероятностей, источником которых является эксперт или группа экспертов, формируются в условиях существования уникальных ситуаций, когда отсутствует предыстория реализации случайных событий.

Такой подход влечет за собой решение задач обработки экспертных оценок, которым в настоящее время посвящена обширная литература.

Наличие факта зависимости (независимости) систем случайных событий определяет порядок построения деревьев вероятностей: наличие независимости позволяет объединить различные системы случайных событий в дерево, в произвольном порядке; зависимость таких систем требует выполнения определённого порядка при их объединении. Приведём формулировки зависимости (независимости) случайных событий. Некоторое событие e_i независимо от события e_j, если вероятность первого не зависит от того, произошло или нет второе событие. В этом случае для проведения расчетов на дереве вероятностей используется известное выражение: p(e_i,e_j) = p(e_i)×p(e_j).

Событие e_i зависимо от события e_j, если его вероятность зависит от того, произошло или нет событие e_j. Вероятность события e_i, определенная при условии, что произошло событие e_j, называется условной вероятностью события e_j: p(e_i/e_j). Отсюда следует, что если события e_i и e_j независимы, то p(e_i/e_j) = p(e_i). Если же два события зависимы, то вероятность их совместного осуществления (пересечения) равна p(e_i 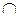e_j) = p(e_j)×p(e_i/e_j).

Наконец, учет числа систем случайных событий имеет важное значение, так как его рост влечёт за собой экспоненциальный рост размеров деревьев вероятностей. Особенно ярко это проявляется, когда число систем случайных событий m>(3 – 4).

Рассмотрим ряд примеров, иллюстрирующих анализ некоторых организационных задач судоремонта с применением деревьев вероятности и вероятностного вывода.

Пример 2.1. Перед судоходной компанией стоит задача выбора судоремонтного предприятия для заключения контракта на выполнение ремонта судов. Дерево вероятностей наиболее значимых рискообразующих факторов, влияющих на заключение контракта, представлено на рис.2.6.

Выполним необходимые вероятностные расчеты на нем. Прежде всего определим вероятности реализации каждого из сценариев с учетом полученных вероятностей каждого из событий, входящих в данный сценарий [10]:

(1):

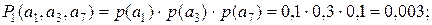
(2):

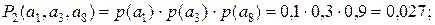
(3):

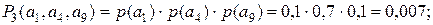
(4):

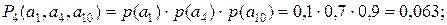
(5): 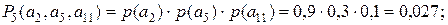(2.9)

(6):

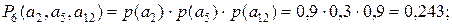
(7):

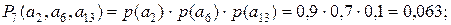
(8):

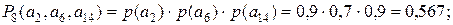
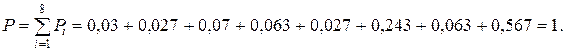
Из рассмотрения полученных результатов можно заключить, что сценарий (8) является самым негативным. Сценарий (1) при приемлемых показателях рискообразующих факторов, обладает минимальной вероятностью своей реализации. Для рассмотренного примера, очевидно, наиболее приемлемым является сценарий (6), однако при этом заказчик должен ради длительности ремонта поступиться его стоимостью и качеством.

Расширим наш анализ посредством определения вероятности появления хотя бы одного из событий, составляющих каждый из сценариев. Для этого обозначим через А событие, состоящее в появлении хотя бы одного из событий a₁, a₂, …, a_n, и воспользуемся следующим выражением из [8]:

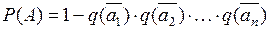, (2.10)

где 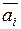– событие противоположное событию a_i, а 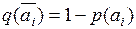– вероятность реализации противоположного события .

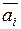Тогда, для каждого из 8-ми рассматриваемых сценариев, имеем:

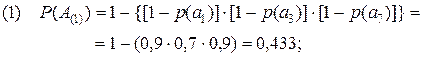
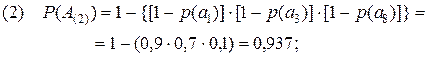
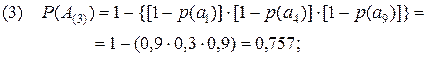
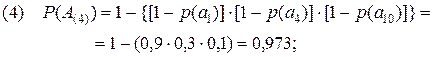(2.11)

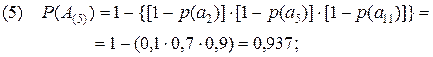
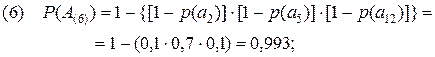
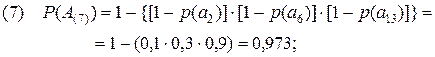
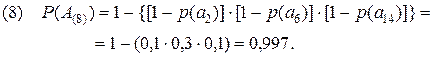
Полученные результаты дополнительно подтверждают сделанные ранее вводы. Так, отрицательная характеристика 8-го сценария усиливается ещё тем, что одно из неприемлемых событий произойдет практически наверняка (P(A₍₈₎)=0,997). Вывод, сделанный в отношении 1-го сценария, подкрепляется низким значением вероятности (P(A₍₁₎)=0,433) одного из трех приемлемых событий. Что же касается 6-го сценария, то его некоторая привлекательность в рассматриваемом примере подтверждается высоким значением вероятности P(A₍₆₎)=0,993 реализуемого события a₅.

Пример 2.2. Рассмотрим задачу вероятностного анализа нацеленного на прогнозирование портфеля заказов судоремонтного предприятия, которое стремится сохранить лидирующее положение на определенном сегменте рынка. Вся исходная информация задачи представлена исходным деревом на рис. 2.7.

Полагается, что ожидаемое состояние портфеля заказов на судоремонт может быть представлено двумя событиями: a₁ – расширение и a₂ – уменьшение портфеля заказов. В зависимости от этого, состояние дел предприятия представляется событиями: b₁ – предприятие сохранит лидирующее положение и b₂ – лидирующее положение может быть потеряно. Для сохранения лидирующего положения на рынке предприятие планирует организовать рекламную компанию, которая может быть связана также с двумя событиями: c₁ – успех; c₂ – неудача.

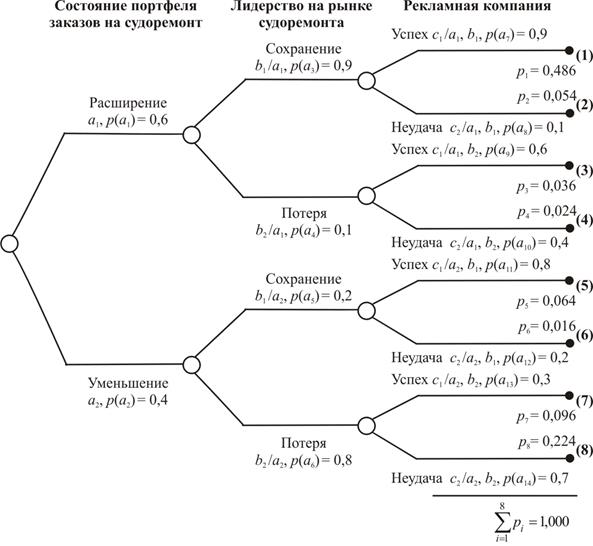
Рис. 2.7. Дерево вероятностей факторов, определяющих лидерство на рынке судоремонта

Приведём технику вычисления вероятностей на примере из работы [10]

Полная вероятность успеха рекламной компании равна:

Р(успех)= P₁+P₃+P₅+P₇=0,486+0,036+0,064,0,096=0,682. (2.12)

Полная вероятность неудачи рекламной компании равна:

Р(неудача)= P₂+P₄+P₆+P₈=0,054+0,024+0,016+0,224=0,318. (2.12)

Полагая, что состояние портфеля заказов и положение на рынке зависят от ожидаемых состояний рекламной компании, перестроим дерево вероятностей, как показано на рис. 2.8.

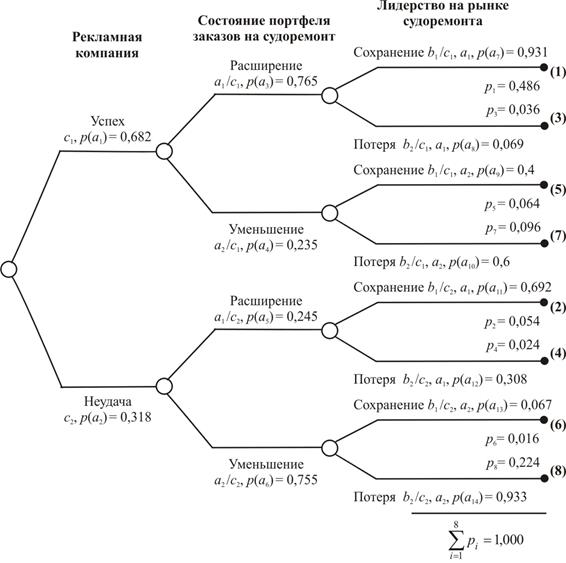
Рис. 2.8. Перестроенное дерево вероятностей

Вероятности событий для такого дерева рассчитаем, используя данные рис. 2.7. Таким образом, имеем:

р¹(с₁)= Р(успех)=0,682; р¹(с₂)= Р(неудача)=0,318.

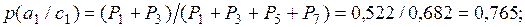
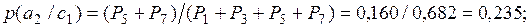(2.13)

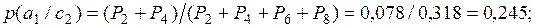
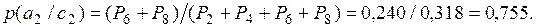
С учетом полученных значений вероятностей, далее получаем:

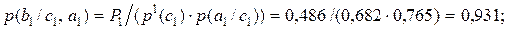
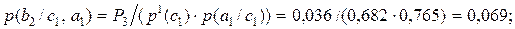
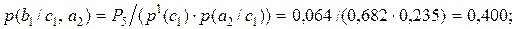
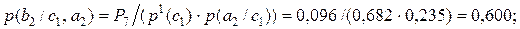(2.14)

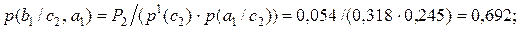
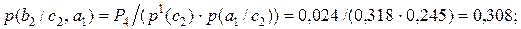
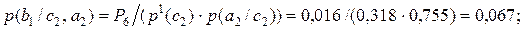
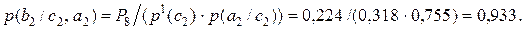
Проведенные расчеты показывают, что вероятность сохранения лидерства на рынке судоремонта при успехе рекламной компании равна P₁+P₅=0,486+0,064=0,550, а вероятность сохранения лидирующего положения при неудаче рекламной компании равна P₂+P₆=0,054+0,016=0,070.

Рассмотренная техника построения деревьев вероятностей и расчета соотношений вероятностного вывода на них может быть с успехом использована для анализа различных организационных и организационно-технических задач судоремонта в условиях неопределенности.